Дальность горизонта с уровня моря

Видимый горизонт и дальность видимости

Расчет видимого горизонта и дальности видимости в зависимости от высоты наблюдателя и наблюдаемого объекта.

Калькулятор ниже предназначен для расчета видимого горизонта и дальности видимости в зависимости от высоты наблюдателя и наблюдаемого объекта. Под ним, как водится, немного теории.

Видимый горизонт и дальность видимости

Видимый горизонт
Так как земля изогнута, наблюдателю, находящемуся, например, в море, представляется, что он находится в центре круга, по краям которого небо как бы смыкается с морской поверхностью. Эта окружность и называется видимым горизонтом наблюдателя. На картинке слева видимый горизонт обозначен пунктирной линией. То есть для наблюдателя, находящегося в точке А на высоте h от земли, видимый горизонт будет образован всеми точками касания лучей зрения земной поверхности (угол BCO равен 90 градусов).

Говоря о видимом горизонте чаще всего имеют в виду длину d отрезка BC. Длину d легко вывести из теоремы Пифагора.

где R — радиус Земли, который обычно принимают за 6378 километров.

В реальной жизни на стороне человека выступает атмосфера. Она, благодаря явлению рефракции, то есть преломлению лучей в верхних слоях атмосферы, расширяет его горизонты примерно на 6% 🙂
Формула, таким образом, принимает вид

В принципе, везде (по крайней мере, насколько я находил в Интернете) для расчетов используют упрощенную формулу, из которой исключен радиус Земли. Она, кстати, вполне выводится из верхней.
, для результата в морских милях или
, для результата в километрах

Дальность видимости
Дальность видимости предметов определяется наибольшим расстоянием, на котором наблюдатель увидит вершину наблюдаемого объекта на линии горизонта. Как видно из рисунка, она зависит как от высоты наблюдателя, так и от высоты наблюдаемого объекта. Собственно, это сумма дальности видимого горизонта наблюдателя и дальности видимого горизонта наблюдаемого объекта. Это довольно важный параметр для навигации.

В калькуляторе я ее вычисляю, а на практике, насколько я понимаю, дальности видимости береговых ориентиров указываются во всяческих лоциях, мореходных таблицах и тому подобном для высоты наблюдателя, равной пяти метрам. Для поправки на фактическую высоту наблюдателя используется «номограмма для расчета дальности видимости предметов в море в дневное время при среднем состоянии атмосферы».

Источник

ВИДИМЫЙ ГОРИЗОНТ И ЕГО ДАЛЬНОСТЬ

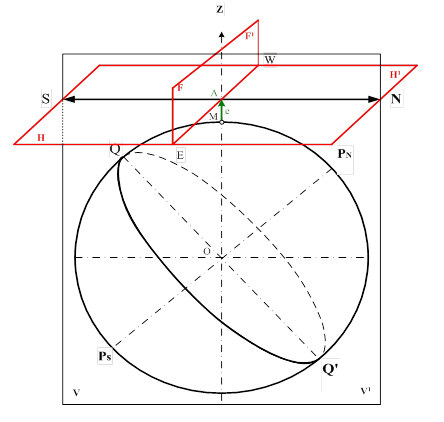
Рис. 4 Основные линии и плоскости наблюдателя

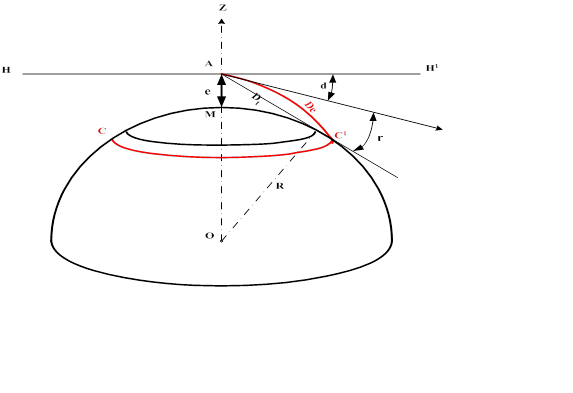
Для ориентирования в море принята система условных линий и плоскостей наблюдателя. На рис. 4 изображен земной шар, на поверхности которого в точке М располагается наблюдатель. Его глаз находится в точке А. Буквой е обозначена высота глаза наблюдателя над уровнем моря. Линия ZMn, проведенная через место наблюдателя и центр земного шара, называется отвесной или вертикальной линией. Все плоскости, проведенные через эту линию, называются вертикальными, а перпендикулярные ей — горизонтальными. Горизонтальная плоскость НН / , проходящая через глаз наблюдателя, называется плоскостью истинного горизонта. Вертикальная плоскость VV / , проходящая через место наблюдателя М и земную ось, называется плоскостью истинного меридиана. В пересечении этой плоскости с поверхностью Земли образуется большой круг РnQPsQ / , называемый истинным меридианом наблюдателя. Прямая, полученная от пересечения плоскости истинного горизонта с плоскостью истинного меридиана, называется линией истинного меридиана или полуденной линией N-S. Этой линией определяется направление на северную и южную точки горизонта. Вертикальная плоскость FF / , перпендикулярная плоскости истинного меридиана, называется плоскостью первого вертикала. В пересечении с плоскостью истинного горизонта она образует линию Е-W, перпендикулярную линии N-S и определяющую направления на восточную и западную точки горизонта. Линии N-S и Е-W делят плоскость истинного горизонта на четверти: NE, SE, SW и NW.

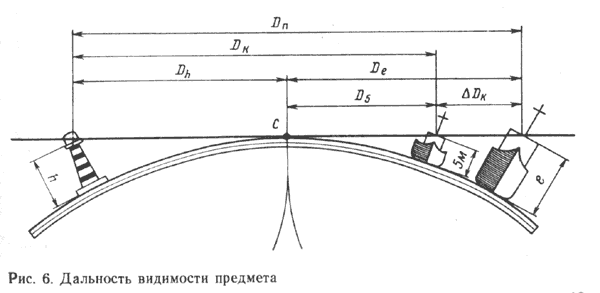
Рис.5. Дальность видимости горизонта

В открытом море наблюдатель видит вокруг судна водную поверхность, ограниченную малым кругом СС1 (рис. 5). Этот круг называется видимым горизонтом. Расстояние De от места судна М до линии видимого горизонта СС 1 называется дальностью видимого горизонта. Теоретическая дальность видимого горизонта Dt (отрезок AB) всегда меньше его действительной дальности De. Это объясняется тем, что из-за различной плотности слоев атмосферы по высоте луч света распространяется в ней не прямолинейно, а по кривой АС. В результате наблюдатель может видеть дополнительно некоторую часть водной поверхности, расположенную за линией теоретического видимого горизонта и ограниченную малым кругом СС 1 . Этот круг и является линией видимого горизонта наблюдателя. Явление преломления световых лучей в атмосфере называется земной рефракцией. Рефракция зависит от атмосферного давления, температуры и влажности воздуха. В одном и том же месте Земли рефракция может меняться даже на протяжении одних суток. Поэтому при расчетах берут среднее значение рефракции. Формула для определения дальности видимого горизонта:

В результате рефракции наблюдатель видит линию горизонта в направлении АС / (рис. 5), касательном к дуге АС. Эта линия приподнята на угол r над прямым лучом АВ. Угол r также называется земной рефракцией. Угол d между плоскостью истинного горизонта НН / и направлением на видимый горизонт называется наклонением видимого горизонта.

ДАЛЬНОСТЬ ВИДИМОСТИ ПРЕДМЕТОВ И ОГНЕЙ. Дальность видимого горизонта позволяет судить о видимости предметов, находящихся на уровне воды. Если предмет имеет определенную высоту h над уровнем моря, то наблюдатель может обнаружить его на расстоянии:

• Dn = Dh + De = 2,08 e + 2,08h (Здесь: Dn в морских милях, e — высота глаза наблюдателя над уровнем моря — в метрах, h — высота предмета над уровнем моря — в метрах).

На морских картах и в навигационных пособиях приводится заранее вычисленная дальность видимости огней маяков Dk с высоты глаза наблюдателя 5 м. С такой высоты De равна 4,7 мили. При е, отличной от 5 м, следует вносить поправку. Её величина равна:

• Dk = 2,08e — 4,7

Тогда дальность видимости маяка Dn равна:

• Dn = Dk + Dk (Здесь: Dn, Dk и Dk в морских милях, e — высота глаза наблюдателя над уровнем моря — в метрах).

Дальность видимости предметов, расчитанная по данной формуле, называется геометрической, или географической. Вычисленные результаты соответствуют некоторому среднему состоянию атмосферы в дневное время суток. При мгле, дожде, снегопаде или туманной погоде видимость предметов, естественно, сокращается. Наоборот, при определенном состоянии атмосферы рефракция может быть очень большой, вследствие чего дальность видимости предметов оказывается значительно больше рассчитанной.

Дальность видимого горизонта. Таблица 22 МТ-75 :

Таблица вычислена по формуле:

Де =2.0809 ,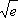

Входя в табл. 22 MT-75 с высотой предмета h над уровнем моря, получают дальность видимости этого предмета с уровня моря. Если к полученной дальности прибавить дальность видимого горизонта, найденную в той же таблице по высоте глаза наблюдателя е над уровнем моря, то сумма этих дальностей составит дальность видимости предмета, без учета прозрачности атмосферы.

Для получения дальности радиолокационного горизонта Дp принято выбранную из табл. 22 дальность видимого горизонта увеличивать на 15%, тогда Дp=2.3930 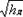. Эта формула справедлива для стандартных условий атмосферы: давление 760 мм, температура +15°C, градиент температуры — 0.0065 градуса на метр, относительная влажность, постоянная с высотой, 60%. Любое отклонение от принятого стандарт­ного состояния атмосферы обусловит частичное изменение дальности радиолокационного горизонта. Кроме того, эта дальность, т. е. расстоя­ние, с которого могут быть видны отраженные сигналы на экране радио­локатора, в значительной степени зависит от индивидуальных особенностей радиолокатора и отражающих свойств объекта. По этим причинам пользоваться коэффициентом 1.15 и данными табл. 22 следует с осторожностью.

Сумма дальностей радиолокационного горизонта антенны Лд и наблюдаемого объекта высотой А представит собой максимальное рас­стояние, с которого может вернуться отраженный сигнал.

Пример 1.Определить дальность обнаружения маяка высотой h=42 м от уровня моря с высоты глаза наблюдателя е=15.5 м.
Решение. Из табл. 22 выбирают:
для h = 42 м . . Дh= 13.5 мили;
для е = 15.5 м . . . . . . Де = 8.2 мили,
следовательно, даль­ность обнаружения маяка
Дп = Дh+Дe = 21.7 мили.

Дальность видимости предмета можно определить также по номограмме, помещенной на вкладыше (приложение 6). MT-75

Пример 2.Найти радиолокационную дальность объекта высотой h=122 м, если действующая высота радиолокационной антенны Hд= 18.3 м над уровнем моря.
Решение. Из табл. 22 выбирают дальности видимости объекта и антенны с уровня моря соответственно 23.0 и 8.9 мили. Суммируя эти дальности и умножая их на коэффициент 1.15, получают, что объект при стандартных условиях атмосферы, вероятно, будет обнаружен с расстояния 36.7 мили.

Источник

Сколько километров до горизонта?

Что такое «горизонт»? Мы часто употребляем это слово, например: солнце скрылось за горизонтом или на горизонте показался автомобиль. Но есть ли научное определение данного термина и можно ли измерять расстояние до горизонта?

Что такое горизонт?

Говоря простым языком, это граница между небом и поверхностью земли или воды. Также иногда можно встретить в определении слово «видимый». Горизонт бывает видимым и истинным.

Видимый горизонт – та часть пространства, которую видит наблюдатель, включая границу между небом и земной поверхностью. Истинный горизонт – воображаемый круг небесной сферы, плоскость которого расположена перпендикулярно относительно вертикальной линии в точке наблюдателя. Его также называют астрономическим или математическим.

Видимый и астрономический горизонт

Расстояние измеряется до видимого горизонта. Для этого используется теорема Пифагора и несложная формула:

Чтобы узнать более-менее точное расстояние, необходимо знать две величины: радиус Земли (R) и высоту, на которой находится наблюдатель (h). Таким образом, очевидно, что чем выше располагается наблюдатель, тем сильнее будет отдаляться линия горизонта.

Примеры расстояния от определенного объекта до горизонта:

• человек ростом 1,75 м, стоящий на земле – 4,7 км;
• крыша 8-этажного дома 25 м – 17,9 км;
• воздушный шар 150 м – 43,8 км;
• самолет 10 км – 357,3 км;
• космический корабль 350 км – 2144 км.

Дальность видимости

Если представить, что наблюдатель стоит на ровной поверхности и ничто не загораживает горизонт, то чем ограничен его кругозор? На открытом пространстве линию горизонта ограничивает выпуклость поверхности Земли, связанная с ее геоидной формой.

Предыдущее изображение показывает, что видимость для наблюдателя заканчивается в той точке, где линия горизонта условно пересекается с геоидной формой Земли. Если наблюдатель поднимется выше, его кругозор расширится.

Возникает вопрос, могут ли различные устройства увеличить дальность видимости? Например, способен ли бинокль расширить кругозор в прямом смысле? Поскольку, бинокль – это оптический прибор, он способен лишь увеличить изображение. Для этого он оснащен специальной конструкцией, которая увеличивает отдаленные объекты, делает их более отчетливыми. Но «заглянуть» за линию горизонта при помощи бинокля нельзя.

Конструкция классического бинокля

Горизонт – граница, разделяющая небо и поверхность земли/воды. Расстояние до видимого горизонта зависит от высоты, на которой находится наблюдатель. Чем выше эта точка, тем сильнее отдаляется горизонт. Например, с высоты среднего человеческого роста (1,75 м) расстояние до горизонта составляет 4,7 км.

Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Источник

Читайте также:  Сеченое сечется море чермное ноты