- Эта статья перенесена сюда!
- Длина дуги параллели
- Длина дуги параллели
- Длина дуги параллели
- Длина дуги параллелей и меридианов на эллипсоиде Красовского, с учетом искажений от полярного сжатия Земли
- В сервисе maps.google.ru, поддерживаемые форматы определяются правилами
- Числовое значение большой экваториальной полуоси – a современных земных эллипсоидов и референц-эллипсоида Красовского
- Таблицы дуг в 1°, 1′, 1″
Эта статья перенесена сюда!
Шарообразная форма Земли и суточное вращение определяют существование на земной поверхности двух неподвижных точек – полюсов. Через полюсы проходит воображаемая земная ось, вокруг которой вращается Земля.
На картах и глобусах проводят самую большую окружность – экватор, плоскость которого перпендикулярна земной оси. Экватор делит Землю на северное и южное полушария. Длина дуги 1° экватора 40075,7 км : 360° = 111,3км.
Параллельно плоскости экватора можно условно расположить множество плоскостей. При пересечении их с поверхностью земного шара образуются малые окружности – параллели. Они проводятся на глобусе или карте на определенном расстоянии от экватора и ориентированы с запада на восток. Длина окружностей параллелей равномерно уменьшается от экватора к полюсам. Напомним, что наибольшая она на экваторе, а на полюсах равна нулю.
Земной шар можно также пересечь воображаемыми плоскостями, проходящими через ось Земли перпендикулярно к плоскости экватора. При пересечении этих плоскостей с поверхностью Земли образуются большие окружности – меридианы. Меридианы можно провести через любые точки земного шара. Все они пересекаются в точках полюсов и ориентированы с севера на юг. Средняя длина дуги 1º меридиана 40008,5 км : 360° = 111 км . Направление местного меридиана в любом пункте можно определить в полдень по направлению тени от гномона или другого предмета. В северном полушарии конец тени от предмета показывает направление на север, в южном – на юг.
Для расчета расстояний на карте или глобусе можно использовать следующие величины: длина дуги 1º меридиана и 1º экватора, равная примерно 111 км .
Чтобы определить расстояние в километрах на карте или глобусе между двумя пунктами, расположенными на одном меридиане, число градусов между пунктами умножают на 111 км . Для определения расстояния в километрах между пунктами, лежащими на одной параллели, число градусов умножают на длину дуги 1° параллели, обозначенную на карте или определенную по таблицам.
Длина дуг параллелей и меридианов на эллипсоиде Красовского
Широта в градусах
Длина дуги параллели в 1° по долготе, м
Широта в градусах
Длина дуги параллели в 1° по долготе, м
Широта в градусах
Длина дуги параллели в 1° по долготе, м
Например, расстояние между Киевом и Санкт-Петербургом, расположенными примерно на меридиане 30°, составляет 111 км *9,5° = 1054 км ; расстояние между Киевом и Харьковом (примерно параллель 50°) – 71 км*6° = 426 км .
Параллели и меридианы образуют градусную сеть. Наиболее точное представление о градусной сети можно получить по глобусу. На географических картах расположение параллелей и меридианов зависит от картографической проекции. Чтобы убедиться в этом, можно сравнить различные карты, например карты полушарий, материков, России, российских регионов и др.
Положение любой точки на земном шаре определяют при помощи географических координат: широты и долготы.
Географическая широта – расстояние вдоль меридиана в градусах от экватора до какой-либо точки земного шара. За начало отсчета широты принят экватор – нулевая параллель. Широта изменяется от 0° на экваторе до 90° на полюсе. К северу от экватора отсчитывают северную широту (с. ш.), к югу от экватора – южную (ю. ш.). На картах параллели надписывают на боковых рамках, а на глобусе – на 0° и 180° меридианах. Например, Харьков расположен на 50° параллели к северу от экватора – его географическая широта 50° с. ш.; острова Кермадек – в Тихом океане на 30° параллели к югу от экватора, их широта примерно 30° ю. ш.
Если на карте или глобусе пункт расположен между двумя обозначенными параллелями, то его географическую широту определяют дополнительно по расстоянию между этими параллелями. Например, чтобы вычислить широту Иркутска, расположенного на карте России между 50° и 60° с. ш., через пункт проводят прямую линию, соединяющую обе параллели. Затем ее условно делят на 10 равных частей – градусов, так как расстояние между параллелями 10°. Иркутск находится ближе к 50° параллели.
На практике географическую широту определяют по высоте Полярной звезды при помощи прибора секстанта, в школе для этой цели используют вертикальный угломер, пли эклиметр.
Географическая долгота – расстояние вдоль параллели в градусах от начального меридиана до какой-либо точки земного шара. За начало отсчета долготы принят гринвичский меридиан – нулевой, который проходит недалеко от Лондона (там, где расположена Гринвичская обсерватория). К востоку от нулевого меридиана до 180° отсчитывают восточную долготу (в. д.), к западу – западную (з. д.). На картах меридианы надписывают на экваторе или верхней и нижней рамках карты, а на глобусе – на экваторе. Меридианы, как и параллели, проводят через одинаковое число градусов. Например, Санкт-Петербург расположен на 30 меридиане к востоку от нулевого меридиана, его географическая долгота 30° в. д.; Мехико – на 100 меридиане к западу от нулевого меридиана, его долгота 100° з. д.
Если пункт расположен между двумя меридианами, то его долготу уточняют по расстоянию между ними. Например, Иркутск расположен между 100° и 110° в. д., но ближе к 100°. Через пункт проводят линию, соединяющую оба меридиана, ее условно делят на 10° и отсчитывают число градусов от 100° меридиана до Иркутска. Следовательно, географическая долгота Иркутска примерно 104°.
Географическую долготу на практике определяют по разнице во времени между данным пунктом и нулевым меридианом или другим известным меридианом. Географические координаты записывают в целых градусах и минутах с указанием широты и долготы. При этом 1º = 60 мин (60′), а0,1° = 6′, 0,2°=12′ и т. д.
- География / Под ред. П.П. Ващенко, Е.И. Шиповича. — 2-е изд., перераб и доп. — К. : Вища шк. Головное изд-во, 1986. — 503 с.
Источник
Длина дуги параллели
Этот онлайн калькулятор вычисляет переводит длину дуги параллели на определенной широте из градусов в метры.
Есть у нас калькулятор, вычисляющий длину дуги меридиана в зависимости от широты, а точнее, длину дуги меридиана размером в одну минуту, более известной как морская миля. Для полноты решил написать калькулятор, рассчитывающий размер длины дуги параллели в зависимости от широты. Из достаточно очевидных соображений, чем больше широта, то есть, чем ближе мы к тому или иному полюсу, тем меньше размер дуги, скажем, в 1 градус, в метрах. Калькулятор ниже и считает размер этой дуги на заданной широте по заданному угловому размеру дуги. Для справки, на экваторе размер дуги параллели в один градус будет максимальным (широта равна нулю) и составит 111 км 319 метров (приближенно). Как это считается, описано под калькулятором.
Длина дуги параллели
Длина дуги параллели
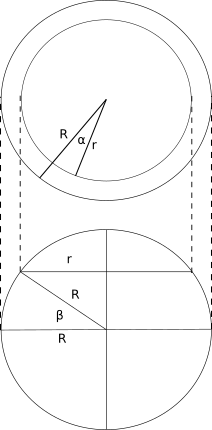
Расчет достаточно простой, и выполняется из общих геометрических соображений. Землю мы конечно приближенно представляем сферой (хотя она геоид).
Чтобы найти длину дуги окружности по углу дуги α, достаточно радиус окружности r умножить на угол дуги в радианах
Для длины дуги в 360 градусов, или 2π радиан, формула превращается в известную всем формула длины окружности
Как видно из рисунка, на определенной широте нас интересует радиус окружности r, полученной при отсечении части сферы плоскостью, параллельной плоскости экватора. На самом экваторе радиус совпадает с радиусом земли R. Выразим интересующий нас радиус через радиус Земли R и заданную широту β:
Соответственно, финальная формула
Ну и в качестве радиуса Земли берем значение, определенное в стандарте WGS-84, а именно, 6378137м. Вот и всё.
Источник
Длина дуги параллелей и меридианов на эллипсоиде Красовского,
с учетом искажений от полярного сжатия Земли
Для определения расстояния по туристической карте, в километрах между пунктами, число градусов умножают на длину дуги 1° параллели и меридиана (по долготе и широте, в системе географических координат), точные расчётные значения которых берутся из таблиц. Приблизительно, с определённой погрешностью, их можно посчитать по формуле, на калькуляторе.
Пример из школьного урока географии (по старому учебнику и из учебного пособия для факультативного курса)
Определить частный масштаб мелкомасштабной (1:1 000 000, 1:6000000, 1:20000000 и мельче) карты земной поверхности (атлас для VI класса) в районе Казани и Свердловска (ныне – Екатеринбург, смотреть список переименованных городов). Оба эти города располагаются, приблизительно, на широте 56° СШ.
Долгота Казани – 49° ВД, Екатеринбурга – 60°ВД.
Расстояние между ними на карте – 1,1 см (определяется с помощью измерительного циркуля и линейки с миллиметровыми делениями).
Длина дуги параллели в 1° для широты 56°СШ – равна 62394 метров.
60 — 49 = 11° (разница в долготах).
L = 62394 * 11 = 686 334 метров = 68 633 400 см (расстояние между пунктами в сантиметрах).
m = 1 / (68 633 400 / 1,1)
Ответ: частный масштаб (m) – в 1 см 624 км.
Главный масштаб (подписанный в зарамочном
оформлении этой карты) – 1 / 75 000 000 (1 см 750км).
Частный м-б может быть и больше и меньше главного, в зависимости от расположения выбранного участка на карте.
Пример перевода числовых значений географических координат из десятых долей в градусы и минуты.
Приближенная долгота города Свердловска – 60.8° (шестьдесят целых и восемь десятых градуса) восточной долготы.
8 / 10 = X / 60
X = (8 * 60) / 10 = 48 (из пропорции находим числитель правой дроби).
Итог: 60.8° = 60° 48′ (шестьдесят градусов и сорок восемь минут).
Чтобы добавить символ градуса ( ° ) – нажмите Альт+248 (цифрами в правой цифровой панели клавиатуры; в ноутбуке – с нажатой спец.кнопкой Fn или включив NumLk). Так делается в операционных системах Windows и Linux, а в ОС Mac – с помощью клавиш Shift+Option+8
Координаты широты всегда указываются перед координатами долготы (и печатая на компьютере, и записывая на бумаге).
Задача. Определить длину параллели на заданной широте, например, 50°
с помощью таблиц длин дуг (референц-эллипсоид Красовского)
www.kakras.ru/mobile/book/dlina-dugi.html
Решение. Из таблицы («Длина дуги параллели в 1°»), для широты 50 градусов, находим соответствующее значение для дуги 1° – 71697 метров.
В окружности – 360 градусов, поэтому, умножаем табличное значение на 360
71697 * 360 = 25 810 920 метров
В сервисе maps.google.ru, поддерживаемые форматы определяются правилами
Примеры, как будет правильно:
Полная форма записи угла (градусы, минуты, секунды с долями):
41° 24′ 12.1674″, 2° 10′ 26.508″
Сокращённые формы записи угла:
Градусы и минуты с десятичными долями – 41 24.2028, 2 10.4418
Десятичные градусы (DDD) – 41.40338, 2.17403
Сервис Гугл-мап имеет онлайн-конвертер для преобразований координат и перевода их в нужный формат.
В качестве десятичного разделителя числовых величин, на сайтах в Интернет и в компьютерных программах – рекомендуется использовать точку.
Числовое значение большой экваториальной полуоси – a
современных земных эллипсоидов и референц-эллипсоида Красовского
Референц-эллипсоид Ф.Н.Красовского, применявшийся в СССР (с 1942 года)
в системах отсчета СК-42 и в РФ (СК-42/95, до 1 января 2017 г.)
a= 6 378 245
ГСК-2011 – эллипсоид и Российская геодезическая система координат 2011 года,
для осуществления геодезических и картографических работ.
a= 6 378 136.5
WGS-84 – современный Международный общеземной эллипсоид отсчетной системы,
почти идентичен ITRF(2008)
a= 6 378 137
Таблицы дуг в 1°, 1′, 1″
Чтобы убедиться, что таблица рассчитана по Красовскому,
посчитаем для нулевой широты (экватор), зная числовое значение
большой экваториальной полуоси для референц-эллипсоида Красовского
a= 6 378 245 метров
1 градус дуги параллели на широте 0°(экватор) =
= ( 2 * 3,14159. * 6378245 ) / 360 = 111321
Приведённые на странице таблицы, будут ещё актуальны, в качестве учебных материалов (к имеющимся учебникам), при использовании старых, советских времён, карт и для приблизительных вычислений.
Длина дуги параллели в 1°, 1′ и 1″ по долготе (по линии запад-восток), метров
| Широта, градус | Длина дуги параллели в 1° по долготе, м | Длина дуги паралл в 1′,м | Длина дуги пар. в 1″,м |
|---|---|---|---|
| 0 | 111321 | 1855 | 31 |
| 1 | 111305 | 1855 | 31 |
| 2 | 111254 | 1854 | 31 |
| 3 | 111170 | 1853 | 31 |
| 4 | 111052 | 1851 | 31 |
| 5 | 110901 | 1848 | 31 |
| 6 | 110716 | 1845 | 31 |
| 7 | 110497 | 1842 | 31 |
| 8 | 110245 | 1837 | 31 |
| 9 | 109960 | 1833 | 31 |
| 10 | 109641 | 1827 | 30 |
| 11 | 109289 | 1821 | 30 |
| 12 | 108904 | 1815 | 30 |
| 13 | 108487 | 1808 | 30 |
| 14 | 108036 | 1801 | 30 |
| 15 | 107552 | 1793 | 30 |
| 16 | 107036 | 1784 | 30 |
| 17 | 106488 | 1775 | 30 |
| 18 | 105907 | 1765 | 29 |
| 19 | 105294 | 1755 | 29 |
| 20 | 104649 | 1744 | 29 |
| 21 | 103972 | 1733 | 29 |
| 22 | 103264 | 1721 | 29 |
| 23 | 102524 | 1709 | 28 |
| 24 | 101753 | 1696 | 28 |
| 25 | 100952 | 1683 | 28 |
| 26 | 100119 | 1669 | 28 |
| 27 | 99257 | 1654 | 28 |
| 28 | 98364 | 1639 | 27 |
| 29 | 97441 | 1624 | 27 |
| 30 | 96488 | 1608 | 27 |
| 31 | 95506 | 1592 | 27 |
| 32 | 94495 | 1575 | 26 |
| 33 | 93455 | 1558 | 26 |
| 34 | 92386 | 1540 | 26 |
| 35 | 91290 | 1522 | 25 |
| 36 | 90165 | 1503 | 25 |
| 37 | 89013 | 1484 | 25 |
| 38 | 87834 | 1464 | 24 |
| 39 | 86628 | 1444 | 24 |
| 40 | 85395 | 1423 | 24 |
| 41 | 84137 | 1402 | 23 |
| 42 | 82852 | 1381 | 23 |
| 43 | 81542 | 1359 | 23 |
| 44 | 80208 | 1337 | 22 |
| 45 | 78848 | 1314 | 22 |
| 46 | 77465 | 1291 | 22 |
| 47 | 76057 | 1268 | 21 |
| 48 | 74627 | 1244 | 21 |
| 49 | 73173 | 1220 | 20 |
| 50 | 71697 | 1195 | 20 |
| 51 | 70199 | 1170 | 19 |
| 52 | 68679 | 1145 | 19 |
| 53 | 67138 | 1119 | 19 |
| 54 | 65577 | 1093 | 18 |
| 55 | 63995 | 1067 | 18 |
| 56 | 62394 | 1040 | 17 |
| 57 | 60773 | 1013 | 17 |
| 58 | 59134 | 986 | 16 |
| 59 | 57476 | 958 | 16 |
| 60 | 55801 | 930 | 16 |
| 61 | 54108 | 902 | 15 |
| 62 | 52399 | 873 | 15 |
| 63 | 50674 | 845 | 14 |
| 64 | 48933 | 816 | 14 |
| 65 | 47176 | 786 | 13 |
| 66 | 45405 | 757 | 13 |
| 67 | 43621 | 727 | 12 |
| 68 | 41822 | 697 | 12 |
| 69 | 40011 | 667 | 11 |
| 70 | 38187 | 636 | 11 |
| 71 | 36352 | 606 | 10 |
| 72 | 34505 | 575 | 10 |
| 73 | 32647 | 544 | 9 |
| 74 | 30780 | 513 | 9 |
| 75 | 28902 | 482 | 8 |
| 76 | 27016 | 450 | 8 |
| 77 | 25122 | 419 | 7 |
| 78 | 23219 | 387 | 6 |
| 79 | 21310 | 355 | 6 |
| 80 | 19394 | 323 | 5 |
| 81 | 17472 | 291 | 5 |
| 82 | 15544 | 259 | 4 |
| 83 | 13612 | 227 | 4 |
| 84 | 11675 | 195 | 3 |
| 85 | 9735 | 162 | 3 |
| 86 | 7791 | 130 | 2 |
| 87 | 5846 | 97 | 2 |
| 88 | 3898 | 65 | 1 |
| 89 | 1949 | 32 | 1 |
| 90 | 0 |
Упрощённая формула расчёта дуг параллелей (без учета искажений от полярного сжатия):
l пар = l экв * cos(Широта).
Длина дуги меридиана в 1°, 1′ и 1″ по широте (по линии север-юг), метров
| Широта, градус | Длина дуги меридиана в 1° по широте, м | в 1′, м | 1″,м |
|---|---|---|---|
| 0 | 110579 | 1843 | 31 |
| 5 | 110596 | 1843 | 31 |
| 10 | 110629 | 1844 | 31 |
| 15 | 110676 | 1845 | 31 |
| 20 | 110739 | 1846 | 31 |
| 25 | 110814 | 1847 | 31 |
| 30 | 110898 | 1848 | 31 |
| 35 | 110989 | 1850 | 31 |
| 40 | 111085 | 1851 | 31 |
| 45 | 111182 | 1853 | 31 |
| 50 | 111278 | 1855 | 31 |
| 55 | 111370 | 1856 | 31 |
| 60 | 111455 | 1858 | 31 |
| 65 | 111531 | 1859 | 31 |
| 70 | 111594 | 1860 | 31 |
| 75 | 111643 | 1861 | 31 |
| 80 | 111677 | 1861 | 31 |
| 85 | 111694 | 1862 | 31 |
| 90 |

Рисунок. 1-секундные дуги меридианов и параллелей (упрощённая формула).
Практический пример использования таблиц. Например, если на карте не указан численный масштаб и нет масштабной линейки, но есть линии градусной картографической сетки – можно графически определить расстояния, из расчёта, что один градус дуги соответствует числовой величине протяжённости, полученной из таблицы. В направлениях «север-юг» (между горизонтальными линиями географической сетки на карте) – значения длин дуг меняются, от экватора до полюсов Земли, незначительно и составляют, приблизительно, 111 километров в одном градусе. Далее, вычислив, сколько содержится в сантиметровом отрезке, можно определить протяжённость произвольного профиля.
Список использованной литературы и ссылки на Интернет-ресурсы
Андреев Н.В. Топография и картография: Факультативный курс. М., Просвещение, 1985
Учебник по математике. Формулы для вычисления длины окружности по её диаметру или радиусу.
Туристический минисправочник по прикладной топографии – определение расстояния между двумя соседними параллелями по «размеру градуса». Здесь можно найти ответ на вопрос из задачи – сколько километров в одном градусе по линии долготы?
Источник
