Учебник по навигации
Глава 1
§ 6. Видимый горизонт и его дальность
Наблюдатель, находясь в море, всегда видит вокруг себя определенный участок земной поверхности, в центре которого находится он сам. Этот участок принято называть кругозором наблюдателя. Границей кругозора наблюдателя является линия, по которой небосвод как бы соприкасается с морем; называется она линией видимого горизонта. С увеличением высоты глаза наблюдателя его кругозор расширяется, линия видимого горизонта отодвигается от наблюдателя, дальность видимого горизонта увеличивается.
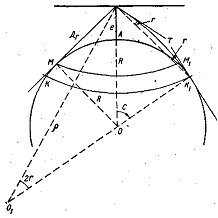
На сферической поверхности Земли линия видимого горизонта представляется малым кругом ММ1 (смотрите рисунок), по которому прямые линии — лучи, проведенные во все стороны от глаза наблюдателя, касаются земной поверхности.
Геометрическая дальность видимого горизонта Дг без учета земной рефракции, представляющая собой сферический радиус AM, может быть рассчитана на основании следующих соображений. Учитывая, что высота глаза наблюдателя е по сравнению с размерами Земли незначительна (на современных кораблях высота глаза едва ли может быть больше 50 м), сферический радиус AM можно считать равным длине касательной ВМ. Тогда из прямоугольного треугольника ОВМ можно написать
Oтношение e / 2R настолько мало, что пренебрежение им практически не скажется на, точности вычисляемой дальности. Учитывая это, можно считать, что
Дг = √ <2re>
Длину сферического радиуса AM и приравненной к нему касательной ВМ мы назвали геометрической дальностью видимого горизонта без учета земной рефракции.
Если бы земная атмосфера во всех своих слоях имела одинаковую плотность (или будь Земля вовсе лишена атмосферы), лучи света от линии видимого горизонта MM1 достигали бы глаза наблюдателя по прямым без искривлений и сферический радиус AM представлял бы фактическую дальность видимого горизонта. В действительности же в земной атмосфере лучи света распространяются не прямолинейно, а с некоторым преломлением вследствие неодинаковой плотности атмосферы в разных ее слоях. Явление преломления светового луча, проходящего через слои земной атмосферы с разной плотностью, называется земной рефракцией. Вследствие рефракции траектория луча, соединяющего малый круг ММ1 с глазом наблюдателя В, в действительности будет кривой линией, обращенной вогнутостью к Земле. Точка касания этого луча с поверхностью Земли будет лежать несколько дальше точки М1, а именно в точке К1. Следовательно, кругозор наблюдателя за счет рефракции расширится и дальность видимого им горизонта увеличится.
Земная рефракция характеризуется углом r земной рефракции, заключенным между хордой ВК1 и касательной к траектории светового луча K1B в точке В. Величина этого угла зависит от преломляющих свойств атмосферы в момент наблюдений, в свою очередь зависящих от разности температуры воды и воздуха, влажности воздуха, атмосферного давления и других факторов. Проходя из более плотных слоев атмосферы у поверхности Земли в менее плотные, на высоте е луч света, преломляясь, искривляется и принимает вид кривой К1В. Поэтому наблюдатель видит точку К1 не по направлению касательной BM1 или хорды BK1, а по направлению касательной ВТ к траектории действительного луча К1В. На сравнительно небольших расстояниях от точки В траекторию луча света можно принять за дугу окружности радиуса ρ . Из многочисленных наблюдений, произведенных в разное время и в разных частях земного шара, установлено, что отношение R / ρ , называемое коэффициентом земной рефракции, при нормальном состоянии атмосферы примерно равно 0,16. Этот коэффициент характеризует преломляющую способность земной атмосферы.
Для отыскания зависимости геометрической дальности видимого горизонта с учетом земной рефракции от высоты глаза наблюдателя е обратимся к рисунку. На этом рисунке действительная дальность видимого горизонта Де представлена сферическим радиусом ВК1 малого круга КК1. Вследствие малости кривизны земной поверхности, а тем более зрительного луча практически можно за дальность видимого горизонта принимать как длину сферического радиуса АК1, так и длину хорды ВК1, а также и сферический радиус ВК1. В треугольнике ОК1В угол ВК1О равен 90 градусов минус r , угол К1ВО равен 90 градусов минус (с-r), ВК1 = Де — геометрическая дальность видимого горизонта с учетом земной рефракции.
Применяя к треугольнику ОК1В теорему синусов, можно написать:
ОВ / sin (90° — r) = ОК1 / sin <90° - (c-r)>
или
R+e / R = cos r / cos (c-r)
Вычтя из правой и левой частей полученного равенства по единице
R+e / R — 1 = cos r / cos (c-r) — 1,
получим
R + e — R / R = cos r — cos (c-r) / cos (c-r);
e / R = cos r — cos (c-r) / cos (c-r).
Заменив в правой части разность косинусов на удвоенное произведение синуса полусуммы на синус полуразности, получим
e / R = 2 sin c/2 sin
По малости углов с и r разложим в ряд sin c/2, sin <(c-2r/2>и cos (c-r), ограничившись при этом первыми членами разложения:
sin (c/2) = c/2; sin
Подставляя в предыдущую формулу результаты разложения, найдем
e/r = 2 * c/2(c-2r/2) = c(c-2r)/2
Но c=Де/R, а 2r=Дe / ρ = ДеR / Rρ = (Де / R) * k, где
k = R / ρ — коэффициент земной рефракции.
С учетом последних замечаний
Разложив (1-к) в минус 1/2 степени в ряд и ограничившись двумя первыми членами разложения, получим
Де = (1+к/2)* √ <2re>
или
Де (мили) = 1,08 * √ <2*6371*е (м) / 1852 * 1852>= 2,08 √ е (м).
Такова формула геометрической дальности видимого горизонта с учетом земной рефракции в море для наблюдателя с высотой глаза, равной е. Для приближенных расчетов можно принимать, что геометрическая дальность видимого горизонта в морских милях равна удвоенному корню квадратному из численного значения высоты глаза наблюдателя в метрах.
В мореходных таблицах имеется специальная таблица 22-а, вычисленная по последней формуле. Пользуясь этой таблицей, можно непосредственно по высоте глаза наблюдателя е выбрать дальность видимого горизонта. Рассмотренные выше геометрические дальности видимого горизонта как с учетом, так и без учета земной рефракции являются дальностями теоретическими. Действительная дальность видимого горизонта в зависимости от условий прозрачности атмосферы может значительно отличаться от теоретической. Действительная дальность видимости может быть определена только опытным путем.
Источник
ВИДИМЫЙ ГОРИЗОНТ И ЕГО ДАЛЬНОСТЬ



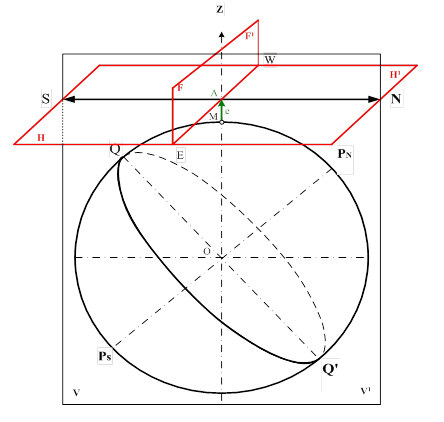
Рис. 4 Основные линии и плоскости наблюдателя
Для ориентирования в море принята система условных линий и плоскостей наблюдателя. На рис. 4 изображен земной шар, на поверхности которого в точке М располагается наблюдатель. Его глаз находится в точке А. Буквой е обозначена высота глаза наблюдателя над уровнем моря. Линия ZMn, проведенная через место наблюдателя и центр земного шара, называется отвесной или вертикальной линией. Все плоскости, проведенные через эту линию, называются вертикальными, а перпендикулярные ей — горизонтальными. Горизонтальная плоскость НН / , проходящая через глаз наблюдателя, называется плоскостью истинного горизонта. Вертикальная плоскость VV / , проходящая через место наблюдателя М и земную ось, называется плоскостью истинного меридиана. В пересечении этой плоскости с поверхностью Земли образуется большой круг РnQPsQ / , называемый истинным меридианом наблюдателя. Прямая, полученная от пересечения плоскости истинного горизонта с плоскостью истинного меридиана, называется линией истинного меридиана или полуденной линией N-S. Этой линией определяется направление на северную и южную точки горизонта. Вертикальная плоскость FF / , перпендикулярная плоскости истинного меридиана, называется плоскостью первого вертикала. В пересечении с плоскостью истинного горизонта она образует линию Е-W, перпендикулярную линии N-S и определяющую направления на восточную и западную точки горизонта. Линии N-S и Е-W делят плоскость истинного горизонта на четверти: NE, SE, SW и NW.
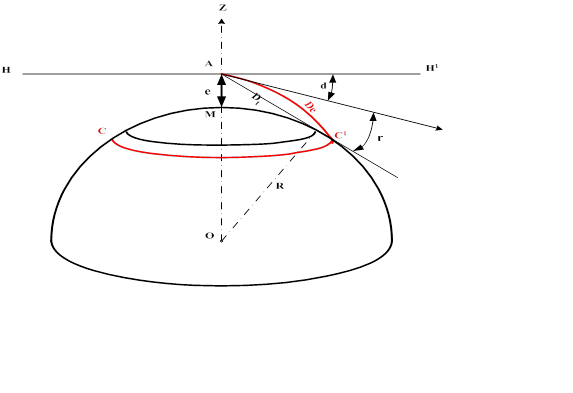
Рис.5. Дальность видимости горизонта
В открытом море наблюдатель видит вокруг судна водную поверхность, ограниченную малым кругом СС1 (рис. 5). Этот круг называется видимым горизонтом. Расстояние De от места судна М до линии видимого горизонта СС 1 называется дальностью видимого горизонта. Теоретическая дальность видимого горизонта Dt (отрезок AB) всегда меньше его действительной дальности De. Это объясняется тем, что из-за различной плотности слоев атмосферы по высоте луч света распространяется в ней не прямолинейно, а по кривой АС. В результате наблюдатель может видеть дополнительно некоторую часть водной поверхности, расположенную за линией теоретического видимого горизонта и ограниченную малым кругом СС 1 . Этот круг и является линией видимого горизонта наблюдателя. Явление преломления световых лучей в атмосфере называется земной рефракцией. Рефракция зависит от атмосферного давления, температуры и влажности воздуха. В одном и том же месте Земли рефракция может меняться даже на протяжении одних суток. Поэтому при расчетах берут среднее значение рефракции. Формула для определения дальности видимого горизонта:
В результате рефракции наблюдатель видит линию горизонта в направлении АС / (рис. 5), касательном к дуге АС. Эта линия приподнята на угол r над прямым лучом АВ. Угол r также называется земной рефракцией. Угол d между плоскостью истинного горизонта НН / и направлением на видимый горизонт называется наклонением видимого горизонта.
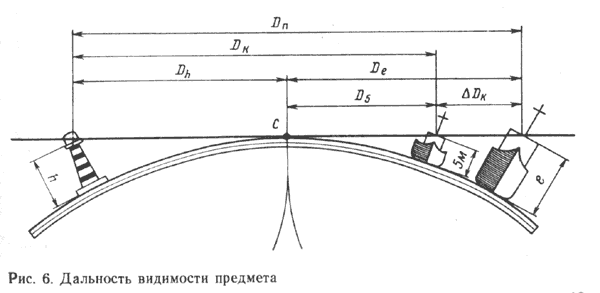
ДАЛЬНОСТЬ ВИДИМОСТИ ПРЕДМЕТОВ И ОГНЕЙ. Дальность видимого горизонта позволяет судить о видимости предметов, находящихся на уровне воды. Если предмет имеет определенную высоту h над уровнем моря, то наблюдатель может обнаружить его на расстоянии:
- Dn = Dh + De = 2,08
e + 2,08
h (Здесь: Dn в морских милях, e — высота глаза наблюдателя над уровнем моря — в метрах, h — высота предмета над уровнем моря — в метрах).
На морских картах и в навигационных пособиях приводится заранее вычисленная дальность видимости огней маяков Dk с высоты глаза наблюдателя 5 м. С такой высоты De равна 4,7 мили. При е, отличной от 5 м, следует вносить поправку. Её величина равна:
Dk = 2,08
e — 4,7
Тогда дальность видимости маяка Dn равна:
- Dn = Dk +
Dk (Здесь: Dn, Dk и
Dk в морских милях, e — высота глаза наблюдателя над уровнем моря — в метрах).
Дальность видимости предметов, расчитанная по данной формуле, называется геометрической, или географической. Вычисленные результаты соответствуют некоторому среднему состоянию атмосферы в дневное время суток. При мгле, дожде, снегопаде или туманной погоде видимость предметов, естественно, сокращается. Наоборот, при определенном состоянии атмосферы рефракция может быть очень большой, вследствие чего дальность видимости предметов оказывается значительно больше рассчитанной.

Дальность видимого горизонта. Таблица 22 МТ-75 :
Таблица вычислена по формуле:
Де =2.0809 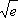
Входя в табл. 22 MT-75 с высотой предмета h над уровнем моря, получают дальность видимости этого предмета с уровня моря. Если к полученной дальности прибавить дальность видимого горизонта, найденную в той же таблице по высоте глаза наблюдателя е над уровнем моря, то сумма этих дальностей составит дальность видимости предмета, без учета прозрачности атмосферы.
Для получения дальности радиолокационного горизонта Дp принято выбранную из табл. 22 дальность видимого горизонта увеличивать на 15%, тогда Дp=2.3930 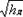
Сумма дальностей радиолокационного горизонта антенны Лд и наблюдаемого объекта высотой А представит собой максимальное расстояние, с которого может вернуться отраженный сигнал.
Пример 1.Определить дальность обнаружения маяка высотой h=42 м от уровня моря с высоты глаза наблюдателя е=15.5 м.
Решение. Из табл. 22 выбирают:
для h = 42 м . . Дh= 13.5 мили;
для е = 15.5 м . . . . . . Де = 8.2 мили,
следовательно, дальность обнаружения маяка
Дп = Дh+Дe = 21.7 мили.
Дальность видимости предмета можно определить также по номограмме, помещенной на вкладыше (приложение 6). MT-75
Пример 2.Найти радиолокационную дальность объекта высотой h=122 м, если действующая высота радиолокационной антенны Hд= 18.3 м над уровнем моря.
Решение. Из табл. 22 выбирают дальности видимости объекта и антенны с уровня моря соответственно 23.0 и 8.9 мили. Суммируя эти дальности и умножая их на коэффициент 1.15, получают, что объект при стандартных условиях атмосферы, вероятно, будет обнаружен с расстояния 36.7 мили.
Источник



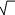 e + 2,08
e + 2,08 Dk = 2,08
Dk = 2,08