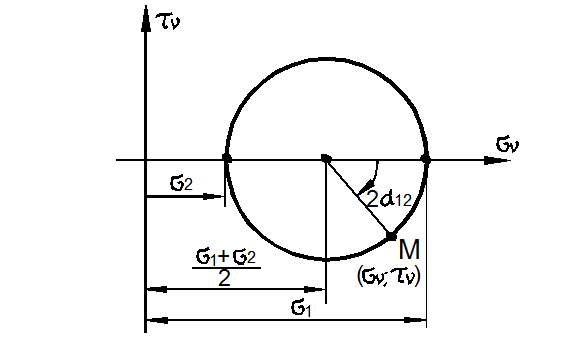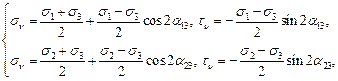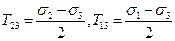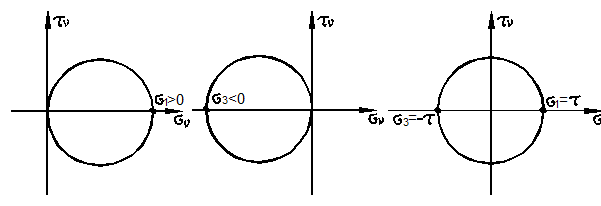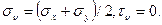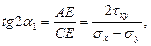Как чертить круги мора

ISopromat.ru

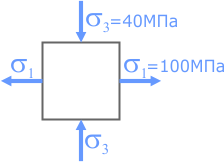
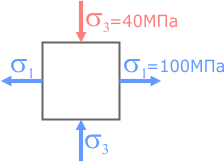
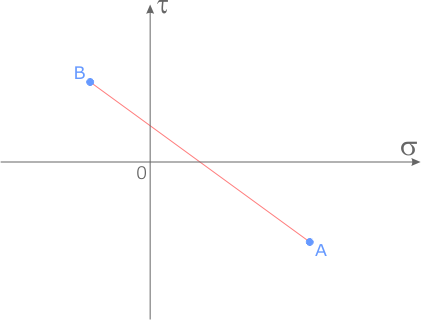
Построить круг Мора для случая плоского напряженного состояния, показанного на следующем рисунке.

На элемент действуют исключительно нормальные напряжения, которые в таком случае называются главными.

Круг Мора строится в плоской системе координат σ-τ .

Для построения круга в данной системе откладываются с учетом их знаков оба напряжения с двух любых смежных площадок (например, верхней и правой) при этом ось напряжений σ необходимо направить вдоль большего (с учетом знака) из нормальных напряжений.

Построение круга Мора

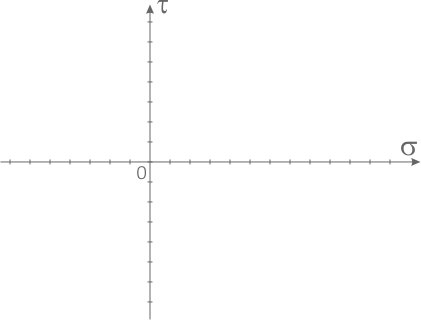
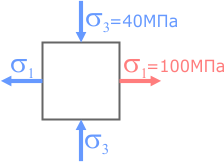
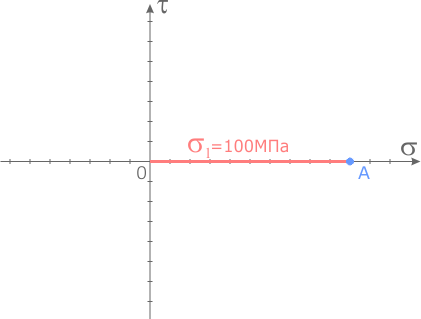
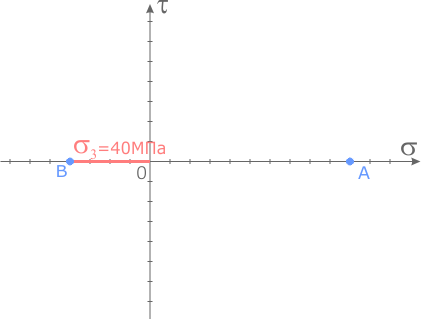
Из центра системы координат откладываем вдоль оси σ значение главного напряжения с правой площадки σ ₁=100МПа.

Так как это напряжение растягивающее оно откладывается в сторону положительных значений.

На конце отрезка ставим точку и обозначаем ее буквой A.

Аналогичные действия выполняются для смежной площадки элемента, но учитывая то, что напряжение на ней сжимающее, т.е. отрицательное ( σ ₃=-40МПа) его величина откладывается влево от пересечения осей.

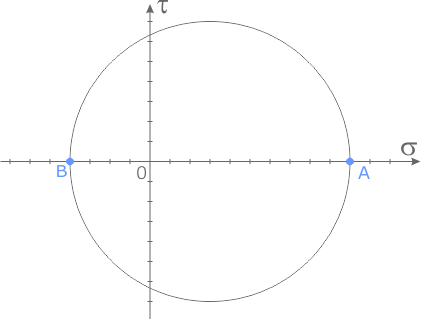
Полученный отрезок AB является диаметром круга Мора.
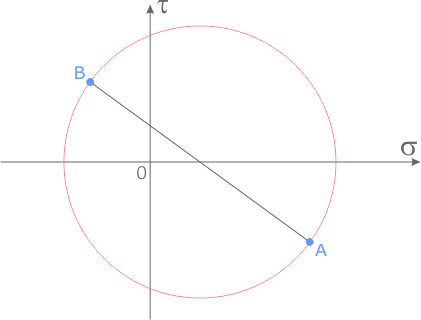
На нем вычерчиваем окружность с центром в середине отрезка AB.

Построение круга Мора по главным напряжениям завершено.

По полученной графике можно с некоторой точностью определить величину и знак нормальных и касательных напряжений для любого положения элемента.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Круг мора и формулы

Круг мора

• Больше кругов Плоское напряженное состояние в определенной точке исследовалось аналитически. Вы также можете легко получить графическое представление, которое можно выразить аналитически до получения всех существующих формул. Для этого представим в качестве координат точки на плоскости XY TA. Чтобы узнать, каково

геометрическое расположение этих точек, используйте: Запишите константы a-St1— и R = -Да, 2 2 в формулах (3.14) и (3.15) Эти выражения принимают следующую форму: х-а + я cos2A; Грех 2А для у = R. (3,19) Уравнение (3.19) представляет собой круговое

уравнение, записанное в параметрической форме, центр которого находится на Людмила Фирмаль

оси o на расстоянии a от начала координат (рис. 89). Этот круг дает геометрическую интерпретацию задачи. Он называется кругом напряжений в честь предложенного немецким ученым Отто Мора или кругом Мора. х Рис 89А Соответствует ли произвольная область наклона, определяемая углом a на окружности, точкой? Мы будем

называть точки, нарисованные на этом сайте. Из уравнения (3.19) углы a и 4-90 ° на окружности напряжений соответствуют двум точкам K и Ri (см. Рисунок 89 в конце того же диаметра). Таким образом, для построения круга достаточно знать координаты этих точек: Od, TA и AA + EO °, TA + 90o == — TA> т.е. на любых двух участках,

• перпендикулярных друг другу. Затем, сосредоточив внимание на положении точки K и оси a-t, можно построить саму окружность напряжений на отрезке KKi, как диаметр. В этом случае вы можете сделать эти сайты. После этого круг родинок строится на точках 1 и 2, лежащих на оси а, как видно из рисунка. 89. 95, фиг. 90 указывает круг Крота, построенный с любым начальным местом и напряжением Тул. И ху-ху-ху ч. Его структура выглядит следующим образом: 1. Для осей

a-t отложить значения нормальных и тангенциальных напряжений в одном и том же масштабе и построить точки изображения в соответствии с координатами вертикальных координат l (a /, Tul) и горизонтальных / Людмила Фирмаль

пересечении окружности и линии является точкой этого участка. Докажите заранее, отметим, что ник. = 2A, центрированный на той же дуге, что и вписанный ^ iM AK-a. = OS + CN = -i- + R cos (? + 2A) = ++ R cos p cos2A-sin p sin 2A. Но так как K, потому что p = CL = -x2—, R sin p = KL = tul_, то _Su-4-I — G V ON— —————— —— c s2A-Tuh Sin 2A. Если мы уравняем полученное уравнение с (3.6), то увидим, что существует CW = a a, который необходимо доказать. Аналогичным образом доказано, что MN-R sin (p4-2A) = R cos p sin2A + R sin p cos2A = sin2A + tuh cos2A = TA. Это позволяет легко графически решить проблему определения напряжения на данной наклонной платформе и обратную задачу

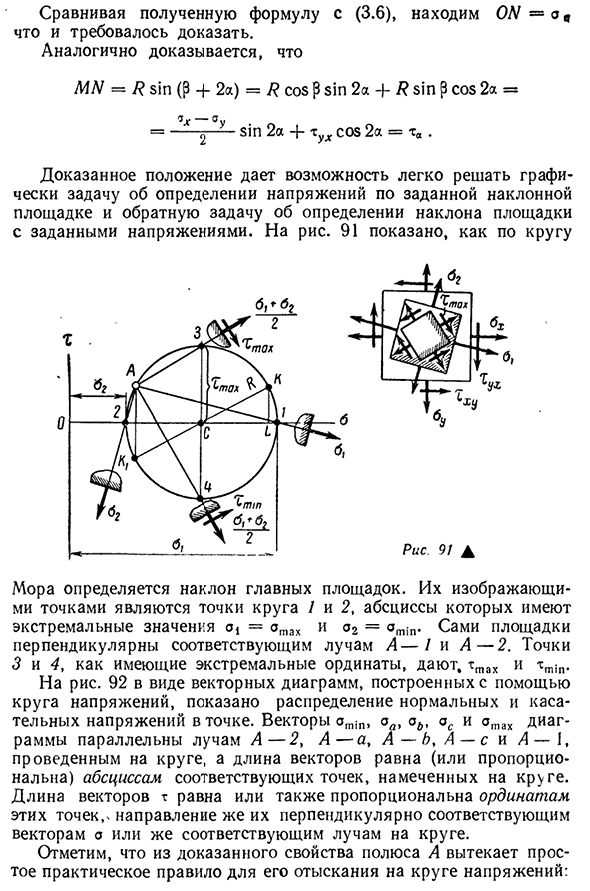
определения наклона площадки из-за данного напряжения. Для риса. 91 показан в виде круга Мора определяется наклоном основного сайта. Точки, которые они представляют, представляют собой круги 1 и 2, и их абсциссы имеют экстремальные значения с = atah и A2 = at! Сама платформа перпендикулярна соответствующим балкам А-1 и А-2. Точки 3 и 4, имеющие экстремальные координаты, ttah и nmin. Для риса. Распределение нормальных и касательных напряжений в точках показано в виде векторной диаграммы, построенной с помощью круга напряжений 92. Иллюстрации векторов amin, OA, GL, AC и amax параллельных лучей A-2, A-a, a- ■ B, A-C и A-1 находятся в круге, а длина вектора — в круге. И т.д. на горизонтальной оси

соответствующей точки Длина вектора t равна или пропорциональна продольной оси этих точек, а его направление перпендикулярно соответствующему вектору a или соответствующему лучу на окружности. Обратите внимание, что проверенные свойства бара означают простое практическое правило нахождения его в круге давления: 4 Заказ № 1037 97 Полюс А находится на пересечении лучей, перпендикулярных исходному участку соответствующей точки формирования изображения К. 90 Эти лучи обозначены пунктирными стрелками. Из круга напряжений нетрудно аналитически установить многие из ранее полученных зависимостей. Так, например (рис. 91), A112 = OS ± R = OS ± V C L2 + # A2 = Это соответствует формуле (3.13) или ^ gpahgp Это соответствует (3.16).

Изучу , оценю , оплатите , через 2-3 дня всё будет на «4» или «5» !

Откройте сайт на смартфоне, нажмите на кнопку «написать в чат» и чат в whatsapp запустится автоматически.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

ISopromat.ru

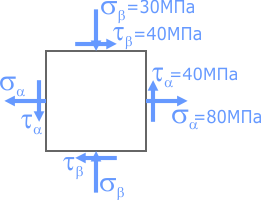
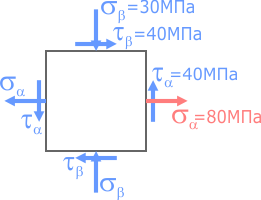
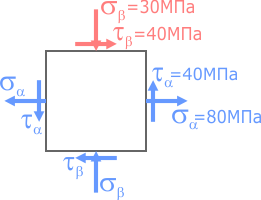
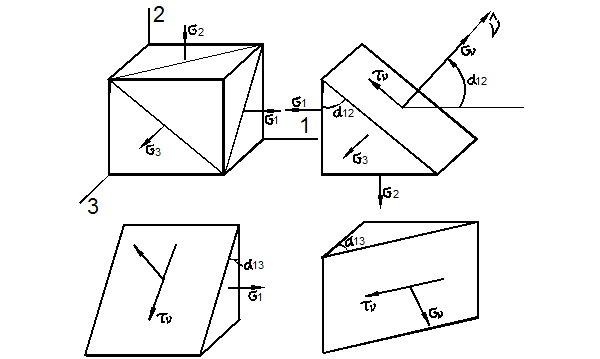
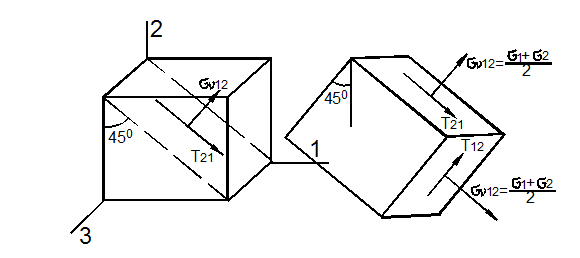
Построить круг Мора для случая плоского напряженного состояния, показанного на рисунке.

Известны направления и значения нормальных и касательных напряжений.

Круг Мора строится в плоской системе координат σ-τ .

Для построения круга потребуются нормальные и касательные напряжения с двух любых взаимно перпендикулярных площадок (например, правой и верхней) при этом ось σ системы направляется вдоль большего (с учетом знака) из нормальных напряжений.

Начнем с правой площадки элемента.
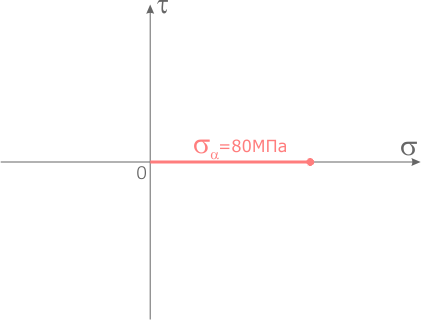
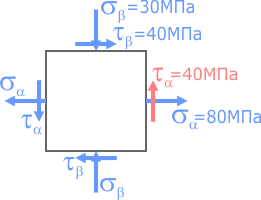
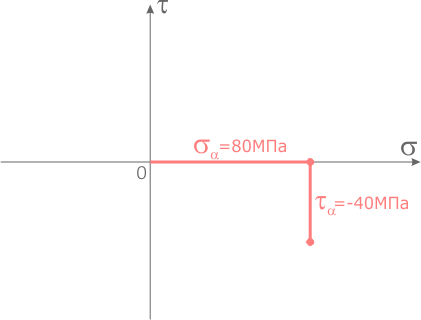
Из центра системы координат отложим вдоль оси σ значение соответствующего нормального напряжения σ_α =80МПа с учетом его знака.

Из конечной точки отрезка отложим вдоль оси τ значение соответствующего касательного напряжения τ_α =40МПа так же с учетом знака.

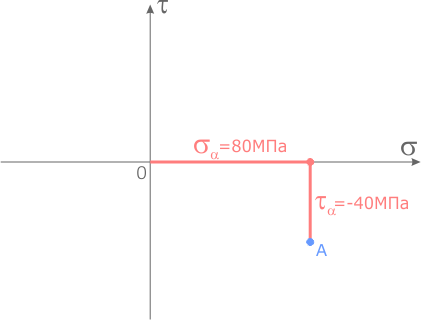
На конце последнего отрезка отметим точку, обозначив ее буквой A.

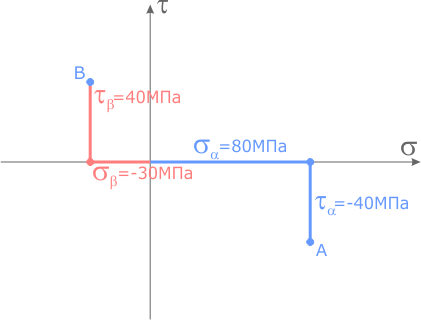
Аналогично для верхней площадки элемента.

Согласно закона парности касательных напряжений, точки A и B всегда будут расположены по разные стороны от оси σ и равноудалены от нее.

Для главных напряжений (при отсутствии касательных) точки A и B останутся на оси нормальных напряжений.

Полученные точки A и B соединяем отрезком.

На отрезке AB как на диаметре вычерчиваем окружность, с центром в точке пересечения отрезка AB с осью σ системы координат.

Круг Мора построен.

Множество точек полученной окружности показывают величину и знак нормальных и касательных напряжений при соответствующем положении площадок элемента.

Точки пересечения круга Мора с осью σ показывают величину и знаки главных напряжений.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Круги напряжений Мора

Удобное двумерное геометрическое представление трёхмерного напряжённого состояния было предложено немецким учёным О. Мором. Отнесём материальную частицу к главным осям (рис. 3.21). Рассечём её плоскостью, содержащей направление третьей главной оси (рис. 3.21,а). Тогда, согласно (35), имеем:

(59)

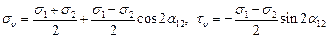
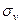
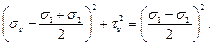
Уравнения (59) представляют собой параметрические уравнения окружности, каноническое уравнение которой имеет в системе координат , вид (рис. 3.22):

(60)

Рис. 3.21

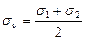
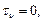
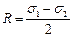
Координаты центра окружности , радиус .

Рис. 3.22

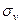
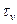
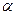
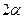
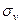
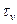
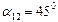
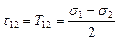
Окружность Мора позволяет графически найти напряжение , на любой площадке, положение которой характеризуется углом . Для этого нужно отложить по часовой стрелке угол и провести под этим углом радиус R до пересечения с окружностью в точке М. Координаты этой точки и есть искомое значения , . Наибольшее касательное напряжение возникает при и равно численно радиусу окружности Мора:

.

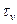
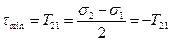
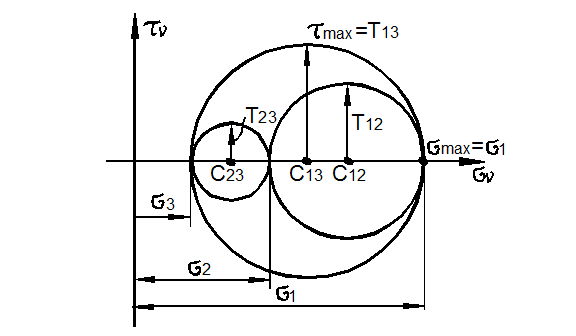
Минимальное значение возникает на площадке при и равно:

.

Аналогичные круги Мора можно построить для наклонных площадок, содержащих главные направления 1 и 2 (рис. 3.23).

Рис. 3.23

Их уравнения в параметрической форме имеют вид:

откуда следует, что наибольшее касательные напряжения в этих случаях:

также равны радиусам соответствующих кругов Мора.

(61)

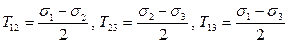
носят название главных касательных напряжений. Они удовлетворяют тождеству

.

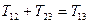
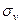
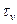
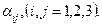
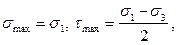
Каждой точке на любой из окружности Мора отвечают напряжения , и площадки, направление которой характеризуется одним из углов Те площадки, которые не содержат ни одну из главных осей, окружностями Мора не описываются. Можно показать, что напряжения на этих площадках задаются точками, расположенными между окружностями в заштрихованной области. Из рис. 3.24 видно, что:

(62)

если принято условие .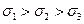

Рис. 3.24

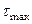
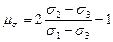
Следовательно, определяется радиусом большого круга Мора. Величину

(63)

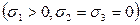
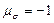
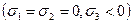
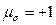
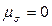
называют параметром вида напряжённого состояния Лоде. При наложении на напряжённое состояние частицы всестороннего давления параметр Лоде не изменяется. Для одноосного растяжения имеем , для сжатия имеем , для плоского чистого сдвига . Соответствующие круги Мора приведены на рис. 3.25.

Таким образом, параметр Лоде 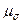характеризует вид напряжённого состояния.

а) б) в)

Рис. 3.25

Если изначально напряжённое состояние не является двухосным, связанным с главными осями, то для построения круга напряжений Мора при плоском напряжённом состоянии следует использовать формулы (35):

(63)

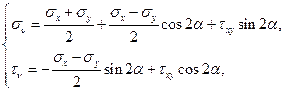
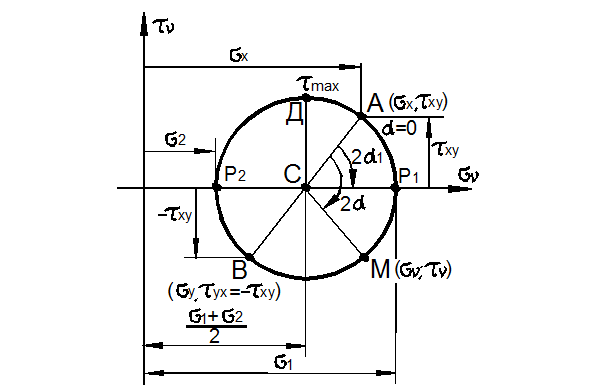
Поступая так же, как и в случае двухосного растяжения сводим параметрические уравнения окружности (63) к каноническому виду (рис. 3.26):

(64)

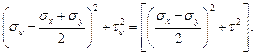
В (64) мы имеем более сложное выражение радиуса окружности:

.

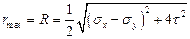
При 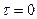уравнение (64) сводится к (60) как частному случаю.

При 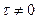построение круга Мора показано на рис. 3.26. Сначала определяется положение центра С круга как точки с координатами

Рис. 3.26

Затем определяется положение точки А, характеризующей напряжения на грани элемента при =0, т.е. . Здесь следует помнить правило знаков для и других напряжений, указанных на рис. 3.12. Заметим, что точки А и В, характеризующие напряжения на площадках, расположенных под углом 90 0 друг к другу, лежат на противоположных концах диаметра круга Мора. Далее на АВ с центром в точке С чертится круг. Напряжения на произвольной площадке, лежащей под углом к оси , можно определить следующим образом. Откладываем от точки А по часовой стрелке угол и определяем положение точки М на круге с искомыми координатами . Точка М’, диаметрально противоположная Д, даёт напряжения для площадки, составляющей угол 90 0 с той, которая имеет нормаль , т.е. для площадки с углом с осью . Точка Д даёт максимальное касательное напряжение, равное радиусу круга Мора:

(65)

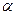
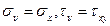
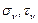
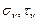
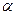
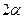
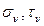
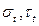
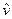
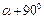
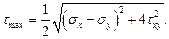
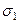
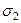
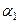
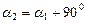
Одной из важных задач использования круга Мора является определение главных нормальных напряжений и . Этим напряжениям отвечают точки Р₁ и Р₂ круга. Из рис. 3.26 следует, что угол между направлениями на точки А и Р₁ равен удвоенному углу , определяющему первое главное напряжение, а угол между направлениями А и Р₂ – удвоенный угол , определяющий второе главное направление. Имеет место соотношение

которое совпадает с формулой (36).

Из изложенного следует, что круг Мора можно использовать в качестве графического способа определения как напряжений на произвольной площадке, так и главных нормальных и максимальных касательных напряжений.

Источник