- Лекции по МОР. Конспект лекций по дисциплине методы оптимальных решений Направление подготовки 080100 Экономика
- Лекция 3. Линейное программирование
- 3.1. Линейное программирование как инструмент математического моделирования экономики
- Выбор модели грунта и её параметров в расчётах геотехнических объектов
- Линейная модель по мору
Лекции по МОР. Конспект лекций по дисциплине методы оптимальных решений Направление подготовки 080100 Экономика
| Название | Конспект лекций по дисциплине методы оптимальных решений Направление подготовки 080100 Экономика |
| Анкор | Лекции по МОР.docx |
| Дата | 02.05.2017 |
| Размер | 1.02 Mb. |
| Формат файла |  |
| Имя файла | Лекции по МОР.docx |
| Тип | Конспект лекций #6625 |
| страница | 7 из 16 |
Подборка по базе: Конспект лекций.doc, Отчет ЛР4 Методы.docx, Реферат по дисциплине пищевые отравления.docx, Вопросы к дифференцированному зачету по дисциплине Информатика.p, Контрольная работа по дисциплине «Экономика гражданского права»., Гимнастика план конспект.docx, 3.2. Методы и средства воспитания.docx, ЗАДАНИЯ ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ ПО ДИСЦИПЛИНЕ Предприниматель, практическая работа по дисциплине ЭкоОснПр (1).docx, Контрольная работа по дисциплине Управление маркетингом.docx Лекция 3. Линейное программирование3.1.Линейное программирование как инструмент математического моделирования экономики. 3.2. Примеры моделей линейного программирования. 3.1. Линейное программирование как инструмент математического моделирования экономикиЛинейное программирование сформировалось как отдельный раздел прикладной математики в 40 – 50-х гг. ХХ в. благодаря работам советского ученого, лауреата Нобелевской премии Л.В. Канторовича. В 1939 году им была опубликована работа «Математические методы организации и планирования производства», в которой он с использованием математики решил экономические задачи о наилучшей загрузке машин, раскрое материалов с наименьшими расходами, распределении грузов по нескольким видам транспорта и другие, предложив метод разрешающих множителей 8 . Л.В. Канторович впервые сформулировал такие широко используемые экономико-математические понятия, как оптимальный план, оптимальное распределение ресурсов, объективно обусловленные оценки, указав многочисленные области экономики, где они могут быть применены. Понятие линейного программирования было введено американским математиком Д. Данцигом, который в 1949 г. предложил алгоритм решения задачи линейного программирования, получивший название «симплексный метод». Математическое программирование, в которое входит линейное программирование, в настоящее время является одним из направлений исследования операций. В зависимости от вида решаемых задач в нем выделяют такие области, как линейное, нелинейное, дискретное, динамическое программирование и др. Термин «программирование» введен в связи с тем, что неизвестные переменные, которые находятся в процессе решения задачи, обычно определяют программу или план работы некоторого экономического объекта. В классическом математическом анализе исследуются общая постановка задачи определения условного экстремума. Однако в связи с развитием промышленного производства, транспорта, агропромышленного комплекса, банковского сектора традиционных результатов математического анализа оказалось недостаточно. Потребности практики и развитие вычислительной техники привели к необходимости определения оптимальных решений при анализе сложных экономических систем. Главным инструментом для решения таких задач является математическое моделирование. При этом сначала строится простая модель, затем проводится ее исследование, позволяющее понять, какие из интегрирующих свойств объекта не улавливаются формальной схемой, после чего за счет усложнения модели обеспечивается большая ее адекватность реальности. Во многих случаях первым приближением к действительности является модель, в которой все зависимости между переменными, характеризующими состояние объекта, являются линейными. Практика показывает, что достаточное количество экономических процессов достаточно полно описывается линейными моделями. Следовательно, линейное программирование как аппарат, позволяющий отыскивать условный экстремум на множестве, заданном линейными уравнениями и неравенствами, играет важную роль при анализе этих процессов. Линейное программирование получило широкое развитие в связи с тем, что было установлено: ряд задач сферы планирования и управления может быть сформулирован в виде задач линейного программирования, для решения которых имеются эффективные методы. По оценкам специалистов примерно 80–85 % всех решаемых на практике задач оптимизации относится к задачам линейного программирования. Созданный математический аппарат в сочетании с компьютерными программами, производящими трудоемкие расчеты, позволяет широко использовать модели линейного программирования в экономической науке и практике. Определение 1 9 . Линейное программирование (ЛП) – это область математического программирования, являющегося разделом математики и изучающего методы поиска экстремальных (наибольших и наименьших) значений линейной функции конечного числа переменных, на неизвестные которой наложены линейные ограничения. Эта линейная функция называется целевой, а ограничения, которые представляют количественные соотношения между переменными, выражающие условия и требования экономической задачи и математически записываются в виде уравнений или неравенств, называются системой ограничений. К задачам линейного программирования сводится широкий круг вопросов планирования экономических процессов, где ставится задача поиска наилучшего (оптимального) решения. Общая задача линейного программирования (ЗЛП) состоит в нахождении экстремального значения (максимума или минимума) линейной функции, называемой целевой 10 : и прямых ограничениях (требовании неотрицательности переменных)
В системе ограничений (3.2) знаки «меньше или равно», «равно», «больше или равно» могут встречаться одновременно. ЗЛП в более краткой записи имеет вид:
Вектор Х = (x1, x2, …, хn) компоненты которого удовлетворяют функциональным и прямым ограничениям задачи называют планом (или допустимым решением) ЗЛП. Все допустимые решения образуют область определения задачи линейного программирования, или область допустимых решений (ОДР). Допустимое решение, которое доставляет максимум или минимум целевой функции f(X), называется оптимальным планом задачи и обозначается f(X * ), где Х * =(x1 * , x2 * , …, хn * ). Еще одна форма записи ЗЛП:
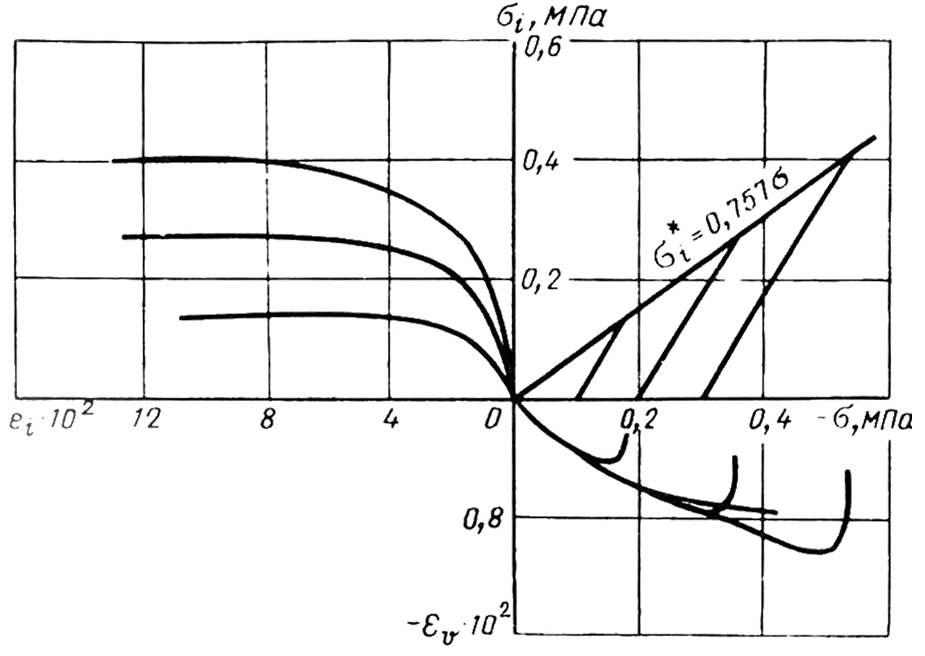
где f(X * ) есть максимальное (минимальное) значение f(С, х), взятое по всем решениям, входящим в множество возможных решений Х. Определение 2 11 . Математическое выражение целевой функции и ее ограничений называются математической моделью экономической задачи. Для составления математической модели необходимо: 1) обозначить переменные; 2) составить целевую функцию исходя из цели задачи; 3) записать систему ограничений, учитывая имеющие в условии задачи показатели и их количественные закономерности. Источник Выбор модели грунта и её параметров в расчётах геотехнических объектовА. И. Голубев АННОТАЦИЯ: Статья посвящена вопросу обоснования выбора математической модели грунта и определению ее параметров. В качестве сопоставляемых моделей выбраны две наиболее популярные упругопластические модели: модель Кулона-Мора и модель упрочняющегося грунта. Приведены результаты методики определения расчетных параметров этих моделей путем сопоставления результатов компьютерного моделирования стабилометрических испытаний в программе PLAXIS с лабораторными данными. В рамках выбранных моделей выполнены расчеты напряженно-деформированного состояния грунтовых массивов с ограждающими конструкциями. Дан анализ выявленных характерных различий в прогнозе деформаций объектов и усилий в конструкционных элементах. 1. Введение Комплексное расчетное обоснование проектов строительства, эксплуатации, реконструкции сооружений в сложных инженерно-геологических условиях, в том числе в стесненной городской застройке, стало невозможным без использования современных компьютерных программ. При этом следует помнить, что расчеты, по результатам которых будет принято проектное решение, следует проводить только после серии предварительных расчетов исследовательского характера, учитывающих влияние ряда факторов при математическом моделировании работы геотехнической системы. Наиболее важными из них являются вопросы создания геометрической модели, конечно-элементной расчетной схемы и выбора модели грунта. В современной практике геотехнических расчетов используются математические модели грунта разной степени сложности. Преимущество простых моделей заключается в меньшем количестве входных параметров, а также в простоте и ясности определяющих уравнений. Однако результаты моделирования в этом случае могут быть достаточно грубыми и плохо согласующимися с реальными данными. Сложные, усовершенствованные модели позволяют описать поведение грунта более точно, но они требуют более широкого набора характеристик грунта, а также достаточной осведомленности и опытности инженера при выборе модели, ее параметров и анализе полученных результатов расчетов. 2. Две альтернативные модели Декларируемый в строительных нормах принцип проектирования по предельным допускаемым деформациям может быть реализован в полной мере только при использовании упругопластических моделей грунта, позволяющих описывать напряженно-деформированное состояние на всем диапазоне изменения нагрузок, вплоть до предельных (разрушающих) значений. Возьмем две такие модели: упругоидеальнопластическую модель (модель Кулона-Мора) (Бугров, 1974) и упругопластическую модель с упрочнением (Schanz et al, 1999). Эти модели включены в программный комплекс PLAXIS, что позволяет провести сравнительный анализ и оценить влияние выбранной модели и ее расчетных параметров на прогнозируемое развитие напряженно-деформированного состояния грунта. При расчетном обосновании многих геотехнических проектов с помощью PLAXIS инженеры часто отдают предпочтение наиболее простой из этих моделей — модели Кулона-Мора (КМ), порой из-за ограниченных данных инженерно-геологических изысканий. Эта модель требует определения всего четырех расчетных параметров грунта: модуля общей деформации Е, коэффициента Пуассона ν, сцепления с и угла трения φ. Модель упрочняющегося грунта (УГ) является усовершенствованной упругопластической моделью, для которой, помимо параметров прочности с и φ, требуется определить модули деформации при первичном нагружении Е и разгрузке Еur, одометрический модуль Еoed, а также показатель степени зависимости жесткости грунта от уровня напряжений m. Эти входные расчетные характеристики жесткости соответствуют определенным эталонным напряжениям, при которых выполнены испытания грунта в стабилометре и одометре. Реальные же характеристики жесткости рассчитываются программой PLAXIS по достигнутым значениям напряжений с учетом развития напряженно-деформированного состояния грунта по гиперболической зависимости. 3. Определение параметров моделей. Лабораторные и виртуальные испытания грунта Выбор расчетной модели грунта и определение ее параметров возможны на основе сопоставления результатов лабораторных испытаний и их виртуальных компьютерных аналогов. На рис. 1 представлены результаты стабилометрических испытаний песка в виде графического паспорта грунта (Зарецкий, 1988). По этим данным, согласно методике определения расчетных характеристик (Brinkgreve et al, 2008), были получены деформационные и прочностные параметры модели КМ и модели УГ (таблица 1). В качестве базовой характеристики жесткости принимается секущий модуль деформации Е50 ref , соответствующий значению бокового давления в стабилометре р ref =100 кПа и 50% прочности грунта. Программа PLAXIS располагает опцией оперативного математического моделирования стандартных лабораторных испытаний грунтов с использованием имеющихся расчетных моделей (опция «soil test»). Рис. 1. Графический паспорт песка Таблица 1. Расчетные параметры моделей грунта Источник Линейная модель по моруВ первой задаче, работа грунта моделировалась при помощи коэффициентов постели, которые были рассчитаны по модели Пастернака: С1=25087.1кН/м 3 , С2=4886.04кН/м. Во второй задаче, грунтовое основания было смоделировано при помощи объёмных КЭ. Данная задача состоит из двух частей: расчет основания в линейной постановке, и с учётом физической нелинейности поведения основания (при задании различных критериев прочности). Компьютерная модель здания и грунтового массива приведена на рисунке 2.
Если грунтовую среду моделировать как линейно деформированную, в ПК «ЛИРА-САПР» реализуется вычисление осадки основания от заданных нагрузок с использованием расчетной схемы в виде линейно деформированного полупространства (задача Буссинеска). В этой модели принимаются два предположения: первое – осадка В отличие от предыдущего метода, модель линейно деформированного полупространства при совместном расчете сооружения с основанием позволяет определить кроме контактных напряжений, напряженно-деформированное состояние почвы всего основания. При таком моделировании основы, с помощью объёмных конечных элементов, в качестве исходных данных вводятся только модуль общих деформаций E, коэффициент Пуассона n и удельный вес каждого слоя. Толщина слоя задается при задании геометрии конечных элементов. При этом расчетная модель фактически сводится к сжатому слою конечной прочности. В рассматриваемой задаче, конечным элементам были заданы следующие характеристики слоев грунтового массива: ИГЭ-1 (E= 28000 кН/м 2 , n = 0,3), ИГЭ-2 (E= 25000 кН/м 2 , n = 0,3), ИГЭ-3 (E= 13000 кН/м 2 , n = 0,3), ИГЭ-4 (E= 16000 кН/м 2 , n = 0,35). Но деформацию грунта можно описать с помощью линейной модели среды лишь до определенного уровня усилий, за пределами которого линейная связь напряжений и деформаций нарушается. Необратимые деформации грунта, как гетерогенной среды, возникают значительно раньше достижения предельного состояния, и они существенно превышают упругие деформации. Поэтому рассмотрим расчет осадки грунтового массива с учетом физически-нелинейной работы основания. При решении этой задачи, для моделирования работы грунта, использовался КЭ273, который позволяет учитывать одностороннюю работу грунта с учетом сдвига. В данном случае, у пользователя есть возможность выбрать модель работы грунта (по Кулону-Мору, Друккеру-Прагеру или Боткину). В рассматриваемом примере, для численного моделирования нелинейных свойств грунтового массива, конечным элементам №273 были заданы следующие характеристики: – ИГЭ-1 (E= 28000 кН/м 2 , n = 0,3, R0= 17,4 кН/м 3 , ke= 1, C= 2 кН/м 2 , Rt= 2 кН/м 2 , Fi= 32˚, Ϭp= 300 кН/м 2 ); – ИГЭ-2 (E= 25000 кН/м 2 , n = 0,3, R0= 19,3 кН/м 3 , ke= 1, C= 1 кН/м 2 , Rt= 1 кН/м 2 , Fi= 30˚, Ϭp= 300 кН/м 2 ); – ИГЭ-3 (E= 13000 кН/м 2 , n = 0,3, R0= 19,1 кН/м 3 , ke= 1, C= 12 кН/м 2 , Rt= 5 кН/м 2 , Fi= 23˚, Ϭp= 280 кН/м 2 ); – ИГЭ-4 (E= 16000 кН/м 2 , n = 0,35, R0= 19,1 кН/м 3 , ke= 1, C= 25 кН/м 2 , Rt= 30 кН/м 2 , Fi= 22˚, Ϭp= 250 кН/м 2 ); где C – сцепление, Rt – предельное напряжение при растяжении, которое было определено из соотношения Простой нелинейной моделью работы почвы является общеизвестная идеально упруго-пластическая модель с предельной поверхностью, что определяется критерием Кулона-Мора. Преимущество модели заключается в простоте назначения параметров, которые можно получить из отчета по инженерно-геологическим изысканиям. Для этой модели условие прочности выражается по формуле: Однако, эта модель предусматривает одинаковое поведение материала на стадии первичного загружения и разгружения, что совсем не характерно для грунтов (в которых модуль загружения и разгружения отличается, как известно, в 5 . 10 раз). Кроме того, недостатком данной модели является то, что в расчёте исключено главное промежуточное напряжение и его влияние на грунт, что не соответствует действительности, а наличие углов на поверхности текучести усложняет численное решение пространственных задач. Эти недостатки исключены при расчёте по критерию прочности Друккера-Прагера. Модель Друккера-Прагера также реализует упругое идеально-пластическое поведение грунтов. А поверхность пластичности согласно модели Друккера-Прагера является правильным круговым конусом относительно гидростатической оси Условие прочности для модели Друкера-Прагера выражают по формуле: Также, в ПК «ЛИРА-САПР» реализовано условие прочности грунта Боткина. Согласно этому условию, в отличии от Кулона-Мора, предполагается, что на прочность почвы влияют все три главных напряжения, а предельное состояние наступает на октаэдрической плоскости (плоскость, является равнонаклонной ко всем главным направлениям напряжений). Условие прочности для модели Боткина: Сравнение и анализ результатов расчета было выполнено по ряду показателей: напряженное состояние наиболее загруженных колонн, величина максимального прогиба консольных стержневых элементов конструкции, кинематические характеристики – перемещение расчетных характерных точек здания по направлению «Z». Численные значения максимальных прогибов консолей для каждого варианта моделирования грунтового основания приведены в таблице 1. Номера секций здания показаны на рисунке 3.
Таблица 1. Максимальные прогибы консольных частей здания, мм Источник |
 (3.1)
(3.1) (3.2)
(3.2) , (3.3)
, (3.3) ,
, ;
;
 ,
,

 точки поверхности основания прямо пропорциональна величине загрузки
точки поверхности основания прямо пропорциональна величине загрузки  в этой точке, второе – осадка распространяется и за пределы площади загружения.
в этой точке, второе – осадка распространяется и за пределы площади загружения. Fi – угол внутреннего трения , Ϭp – предельное напряжение сжатия.
Fi – угол внутреннего трения , Ϭp – предельное напряжение сжатия.
 в пространственной системе главных напряжений.
в пространственной системе главных напряжений.

