Линейная огибающая кругов мора

Теория прочности мора (пятая гипотеза прочности)

Теория прочности мора

• Теория прочности Мора Во всех вышеприведенных теориях критерием прочности принималось значение любых факторов, таких как напряжение, удлинение, энергия и др. При этом предельные значения этих факторов считались постоянными для одного и того же материала и не зависящими от типа напряженного состояния. В

теории кротовой прочности, в отличие от вышеприведенной теории, установлено, что прочностные характеристики материала в некоторой степени зависят от типа напряженного состояния. Получить такую зависимость и оправдать Рис 325Л Для космоса постройте три круга напряжения Используйте предложенный

Мором круг напряжений, равновесное состояние, как(рис. 325). Однако здесь Людмила Фирмаль

мы рассматриваем приближение, которое, основываясь на существующих экспериментах, не учитывает влияние напряжения а*, а прочностные характеристики материала связаны только с напряжением- * Эксперимент показывает, что погрешность от игнорирования напряжения А2 не превышает 10-15%. Таким образом, только один из трех кругов, то есть самый большой, считается 379A3. Этот круг Мор называл главным кругом. С в случае напряжения тока?! И О3 встречает государство окончательного давления материала,

соответствуя основной круг также вызван пределом. В качестве примера приведем рисунок. 326 представляет три предельных круга для материалов, которые были испытаны на растяжение, сжатие и кручение. В то же время было установлено, что предельное напряжение при сжатии, которое указывает на АОС, больше, чем АОР при растяжении, то есть АОС кор. Когда вы рисуете огибающую этих кругов, это обычно кривая, которая пересекает ось a в определенно

• точке C. Эта точка соответствует полному растяжению с предельным напряжением, определяемым абсциссой точки с (см. Рисунок). 326). Кротовая окружность в этом случае превращается в точку, так как напряжения A1, A2 и a3 равны друг другу. Итак, если у вас есть некоторый предельный круг и его оболочка, вы можете предположить, что напряженное состояние, которое является

основным кругом, связанным с оболочкой, также является пределом. Для риса. 326 указывает на то, что семья имеет предел различных комбинаций субъектов с точки зрения подверженности стрессу. Как видно из рисунка, огибающая окружности определяет зависимость этих напряжений от типа напряженного состояния. Таким образом, на практике фактическая огибающая заменяется только касательными в двух окружностях, построенных по опыту растяжения и сжатия, поскольку получение фактической

огибающей предельного круга, построенного для всех возможных напряженных состояний, требует экспериментального исследования этих Людмила Фирмаль

напряженных состояний. 327). Эти линии служат границей региона Государственный 380prochnostnyh. При этом устанавливается линейная зависимость между напряжением и О3, основной круг которой касается этих линий:°1+6а3. (12.34) такое уравнение основано на простой геометрической зависимости, вытекающей из сходства треугольников в связи, вытекающей из сходства DL3CC2 и^A1C1C2 327). Учитывая Ники, вы можете испечь:^? И, Треугольник- Куда? (12.36 утра)) (12.35 утра)) Замена значения(12.36) (12.35) приводит к простому преобразованию в уравнение (12.34). Поскольку последнее должно быть верно в случае растяжения и сжатия, не прибегая к указанному преобразованию, коэффициенты a и Z3 для любой

Изучу , оценю , оплатите , через 2-3 дня всё будет на «4» или «5» !

Откройте сайт на смартфоне, нажмите на кнопку «написать в чат» и чат в whatsapp запустится автоматически.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Теория прочности Мора

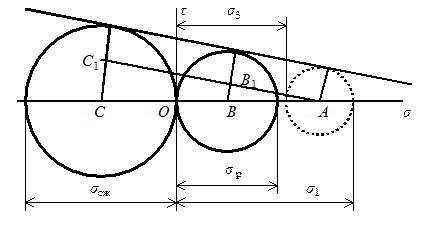
В отличии от рассмотренных выше классических теорий, используется не один, а два критерия: нормальное и касательное напряжения. Окончательно теория сформулирована Отто Мором20 в 1900 году. В ее основании лежит логическое описание явления перехода материала в предельное состояние с помощью кругов напряжений. Из трех кругов напряжений (рис. 6.5) учитывается только наибольший, построенный на отрезке [σ₁, σ₃] как на диаметре в координатных осях σ и τ.

Предположим, что задано некоторое напряженное состояние, для которого можно вычертить наибольший круг напряжений. Если увеличивать пропорционально одному параметру все компоненты, то рано или поздно напряженное состояние станет предельным, для которого и строится круг предельных напряжений. Теперь допустим, что проведено большое число испытаний при различных напряженных состояниях и для каждого из них установлено предельное состояние. В результате можно построить семейство кругов предельных состояний, к которым вычерчивается огибающая линия предельных кругов Мора, которая считается единственной для данного материала. Практически, вместо огибающей, используется её схематизированное приближение, построяемое на основе экспериментов с образцами материала при одноосном растяжении и сжатии. огибающая линия при этом заменяется касательной к предельным кругам Мора при растяжении (круг В) и при сжатии (круг С), отвечающим результатам названных испытаний (рис. 6.5).

Рис. 6.5. Касательная кругов Мора, играющая роль огибающей линии.

Далее необходимо найти величину эквивалентного напряжения, соответствующего теории Мора. С этой целью будем считать, что для исследуемого материала схематизированная огибающая кругов Мора задана в виде касательной к кругам B и С. Найдем зависимость между главными напряжениями σ₁ и σ₃ заданного предельного напряженного состояния (состояния А, показанного пунктиром на рис. 6.5) и равно опасного ему одноосного состояние растяжения.

Восстановим перпендикуляры, в точках касания трех кругов с касательной к ним, которые совпадут с радиусами этих кругов (см. рисунок). Из точки A проведем прямую АС1, параллельную касательной. Из подобия треугольников АСС₁ и АВВ₁ следует:

. (a)

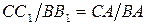
Из того же рисунка непосредственно следует, что:

, ,

, , (b)

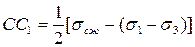
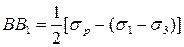
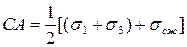
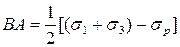
где σ_ри σ_сж –– предельные напряжения материала при растяжении и сжатии.

Подставив выражения (b) в равенство (a), после упрощений получим:

. (c)

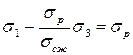
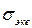
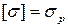
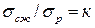
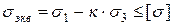
Обозначим: как — левую часть равенства (c), и отношение . Тогда условие прочности, записанное согласно теории прочности Мора, примет вид:

, (6.10)

где [σ] — допускаемое напряжение материала при одноосном растяжении. Если материал пластичен и одинаково сопротивляется растяжению и сжатию, то, приравнивая σ_сж величине σ_р, получим 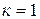и выражение (6.10) в этом случае совпадет точно с выражением (6.5), полученном нами ранее, при рассмотрении 3-й теории прочности.

Теория Мора в настоящее время считается общепризнанной. Она оправдывает себя как для пластичных, так и для хрупких материалов, но, преимущественно, для напряженных состояний смешанного типа, то есть когда отношение 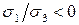. Отличительной чертой теории Мора от рассмотренных ранее классических теорий является тот факт, что она полностью опирается на экспериментальные данные и по мере их накопления может уточняться. Основные недостатками теории Мора:

Первое, это отсутствие влияния промежуточного главного напряжения σ₂ (как и в третьей теории).

Второй недостаток — это трудности в связи с построением огибающей линии предельных кругов Мора.

15 Галилей Галилео (1564 — 1642) — итальянский физик, механик, астроном, математик. В его сочинениях (1638) содержатся вопросы, касающиеся: прочности растянутых и изгибаемых брусьев, геометрически подобных тел, балок равного сопротивления и др.

16 мариотт Эдм(1620 –– 1684) –– французский ученый, изучавший прочность материалов и их упругие свойства. Исходил из теории прочности, критерием разрушения в которой является достижение материалом предельного удлинения. Получил формулу для определения прочности труб на разрыв под действием внутреннего давления.

17 Кулон Шарль Огюстен (1736 –– 1806) –– французский ученый. Занимался испытанием материалов на растяжение, срез и изгиб. Он имел ясное представление о распределении внутренних сил по поперечному сечению.

18 Бельтрами Эудженно(1835 — 1900) — итальянский математик.

20 См. в сноске 13.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Круг Мора, главные напряжения

Чтобы определить напряжения по наклонным сечениям, можно также воспользоваться графическим методом. Суть метода заключается в следующем: строится система координат; на оси икс откладываются нормальные напряжения, на оси игрек откладываются касательные напряжения. В нашем случае на выбранной площадке действуют только нормальные напряжения σx и σy, причём σy является бОльшим напряжением. Далее откладываются точки с координатами (σx;0) и (σy;0). Далее находится точка посередине между ними и на ней, как на центре, строится окружность диаметром (σy-σx):

В предыдущем уроке для нахождения напряжений по наклонным сечениям угол альфа брался от оси икс, точнее от напряжения в этом направлении. Здесь же необходимо отложить удвоенный угол, два альфа, и отложить его от точки А в направлении против часовой стрелки. В итоге получится точка на окружности, координаты которой будут представлять из себя нормальное и касательное напряжение, действующее по данной наклонной площадке:

Можно показать, что:

Из построения определим длину OE:

Определим длину DE:

Полученные выражения совпали с формулами, выведенными в предыдущем уроке.

Из построения видно, что касательные напряжения на двух взаимно перпендикулярных площадках равны по модулю, но противоположны по направлению:

В этом можно убедиться, воспользовавшись формулой:

По аналогии можно получить формулы для нормальных напряжений на площадке +90 градусов:

Данная графическая интерпретация напряжённого состояния в материале называется кругом Мора.

Кругом Мора удобно пользоваться и для решения обратной задачи. Например, рассмотренный ранее случай наддува обшивки фюзеляжа самолёта всегда сопровождается и другими типами нагружения: фюзеляж самолёта изгибается, закручивается и т.д. В итоге к напряжениям от наддува добавляются нормальные и касательные напряжения от изгиба, касательные напряжения от кручения и т.д., что приводит элемент обшивки в следующее напряжённое состояние:

Бывает, что необходимо определить то, на какой угол надо повернуть данный элемент, чтобы по граням элемента действовали только нормальные напряжения. Такие нормальные напряжения, на площадках которых не действует касательных напряжений, будем называть главными. Определим главные напряжения для вышеприведённого элемента, используя круг Мора:

Имея центр в точке C и радиусы CD и CD1, можно достроить окружность:

Условимся обозначать главные напряжения σ1 и σ2, причём σ1 всегда больше σ2.

Из рисунка имеем:

Направление главных напряжений можно получить из рисунка. Известно, что угол DCA есть удвоенный угол между напряжением σ1 и осью икс, и так как 2α измерено от A к D против часовой стрелки, то направление σ1 должно быть следующим (см. рисунок ниже). Это можно проверить, если решать обратную задачу нахождения касательных напряжений по наклонным площадкам.

Для определения числового значения угла из рисунка имеем:

Что касается знака, то он должен быть взят отрицательный, так как он измерен от оси икс по часовой стрелке. Следовательно, получим:

Полученные выше напряжения – главные, и они являются максимальными. Что касается максимальных касательных напряжений, то они определяются величиной радиуса круга:

Источник