- Перемножение эпюр по правилу, методу или способу Мора-Верещагина: формула, таблица, примеры и задачи
- Верещагин и его метод, правило или способ
- Площадь и центр тяжести эпюр
- Перемножение эпюр по Верещагину
- Прямоугольник на прямоугольник
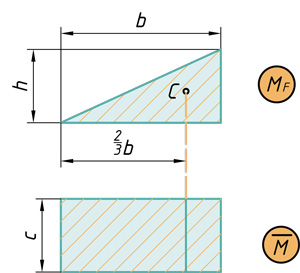
- Прямоугольник на треугольник
- Треугольник на прямоугольник
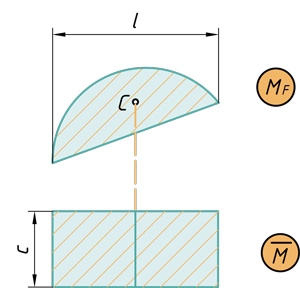
- Сегмент на прямоугольник
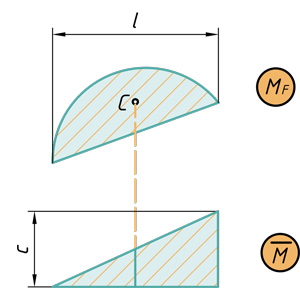
- Сегмент на треугольник
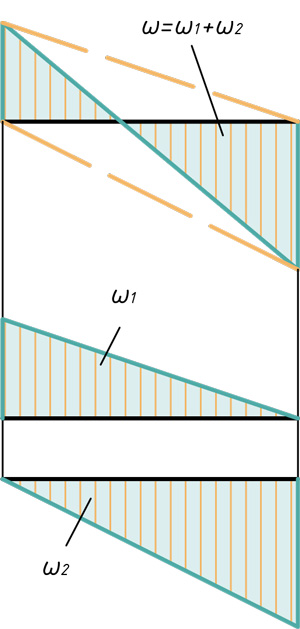
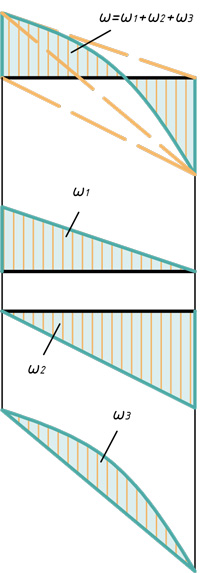
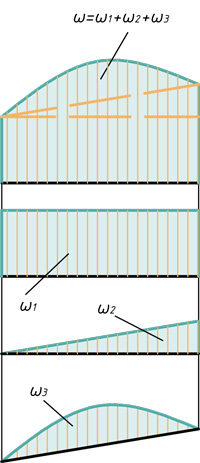
- Частные случаи расслоения эпюр на простые фигуры
- Прямоугольник и треугольник
- Два треугольника
- Два треугольника и сегмент
- Треугольник, прямоугольник и сегмент
- Пример определения перемещений: прогибов и углов поворотов по Верещагину
- Построение эпюры изгибающих моментов
- Построение единичных эпюр моментов
- Перемножение участков эпюры по Верещагину
- Определение прогиба сечения С
- Определение угла поворота сечения С
- Метод мора
Перемножение эпюр по правилу, методу или способу Мора-Верещагина: формула, таблица, примеры и задачи
Привет! В этой статье будем учиться определять перемещения поперечных сечений при изгибе: прогибы и углы поворотов, по методу (способу, правилу) Верещагина. Причем, это правило широко используется не только при определении перемещений, но и при раскрытии статической неопределимости систем по методу сил. Я расскажу, о сути этого метода, как перемножаются эпюры различной сложности и когда выгодно пользоваться этим методом.
Верещагин и его метод, правило или способ
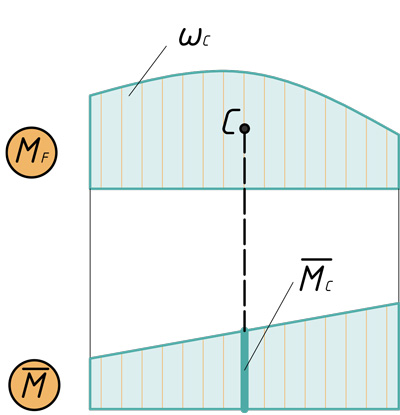
А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть любой. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем не важно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:
Проиллюстрировано перемножение эпюр по Верещагину: C — центр тяжести первой эпюры, ωс — площадь первой эпюры, Mc — ордината второй эпюры под центром тяжести первой.
Площадь и центр тяжести эпюр
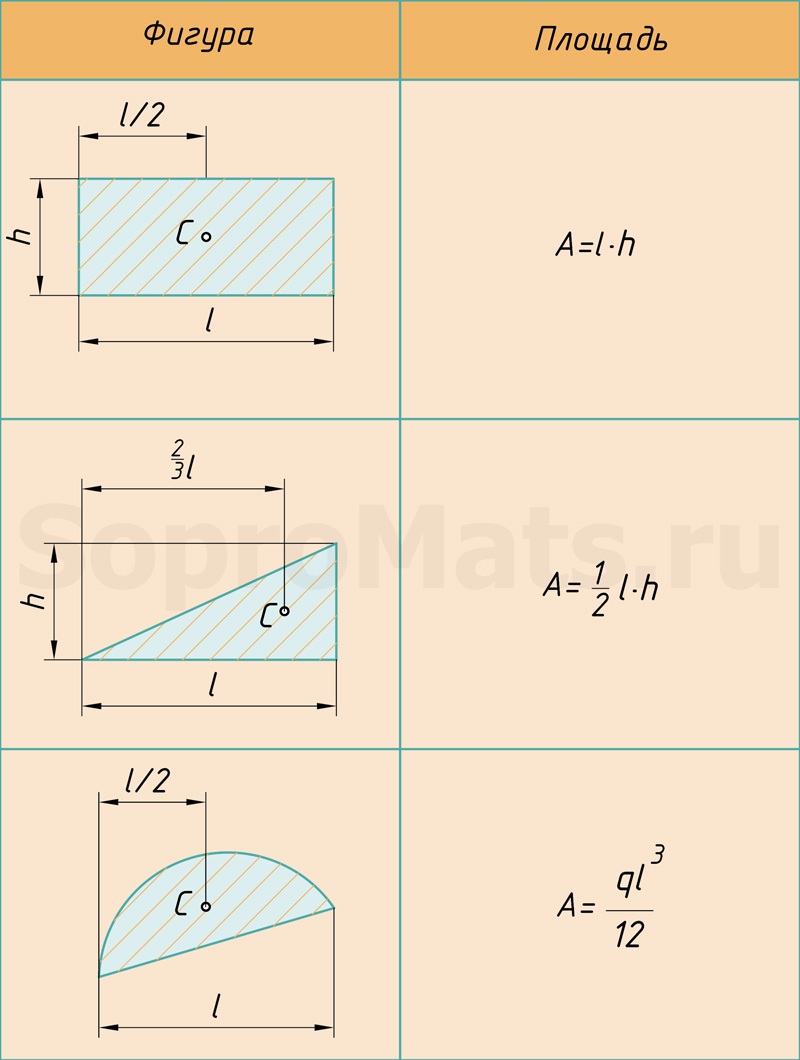
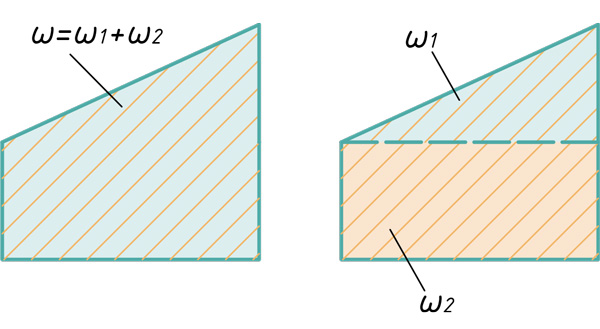
При использовании метода Верещагина, берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.
Любую эпюру можно расслоить всего на три фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.
Поэтому именно с этими фигурами будем дальше работать. Напомню, как вычислить их площадь и где у них находится центр тяжести. Все формулы и размеры оформил в виде таблицы:
Перемножение эпюр по Верещагину
В этом блоке статьи покажу частные случаи перемножения эпюр по Верещагину.
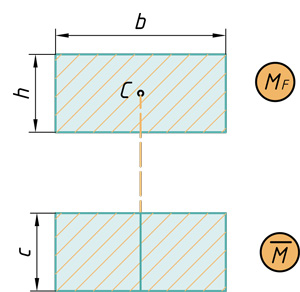
Прямоугольник на прямоугольник
Прямоугольник на треугольник
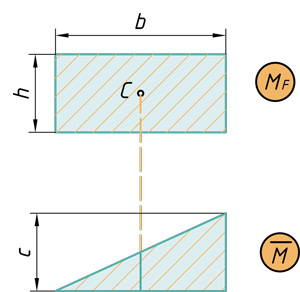
Треугольник на прямоугольник
Сегмент на прямоугольник
Сегмент на треугольник
Частные случаи расслоения эпюр на простые фигуры
В этом блоке статьи покажу частные случаи расслоения эпюр на простые фигуры, для возможности их перемножения по Верещагину.
Прямоугольник и треугольник
Два треугольника
Два треугольника и сегмент
Треугольник, прямоугольник и сегмент
Пример определения перемещений: прогибов и углов поворотов по Верещагину
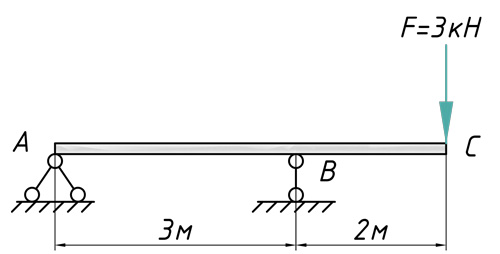
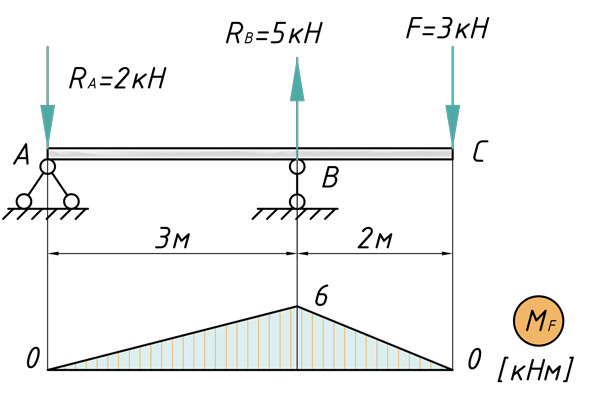
Теперь предлагаю рассмотреть конкретный пример с расчетом перемещений поперечных сечений: их прогибов и углов поворотов. Возьмем стальную балку, которая загружена всевозможными типами нагрузок и определим прогиб сечения C, а также угол поворота сечения A.
Построение эпюры изгибающих моментов
В первую очередь, рассчитываем и строим эпюру изгибающих моментов:
Построение единичных эпюр моментов
Теперь для каждого искомого перемещений необходимо приложить единичную нагрузку (безразмерную величину равную единице) и построить единичные эпюры:
- Для прогибов, прикладываются единичные силы.
- Для углов поворотов, прикладываются единичные моменты.
Например, после расчета величина прогиба получилась положительной, это значит, что направление перемещения сечения совпадает с направлением ранее прикладываемой силы. Тоже самое касается и углов поворотов.
Перемножение участков эпюры по Верещагину
После проведения всех подготовительных работ: построения эпюры изгибающих моментов, расслоения ее на элементарные фигуры и построения единичных эпюр от нагрузок, приложенных в местах и направлении искомых перемещений, можно переходить непосредственно к перемножению соответствующих эпюр.
Определение прогиба сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем прогиб сечения C по методу Мора — Верещагина:
\[ < V >_< C >=\frac < 1 >< E< I >_ < x >> (\frac < 1 > < 2 >\cdot 6\cdot 3\cdot \frac < 2 > < 3 >\cdot 2+\frac < 1 > < 2 >\cdot 6\cdot 2\cdot \frac < 2 > < 3 >\cdot 2)=\frac < 20кН< м >^ < 3 >>< E< I >_ < x >> \]
Представим, что рассчитываемая балки имеет поперечное сечение в виде двутавра №24 по ГОСТ 8239-89, тогда прогиб балки будет равен:
Определение угла поворота сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем угол поворота сечения C по правилу Мора — Верещагина:
Источник
Метод мора
Содержание:
Метод Максвелла — Мора представляет собой универсальный способ для определения линейных и угловых перемещений в любых плоских и пространственных системах.
- Напомним основные этапы использования метода Максвелла -Мора.
При отыскании линейного перемещения к системе, освобожденной от заданных нагрузок, в направлении искомого перемещения (в заданной точке) прикладывается безразмерная единичная сила. Аналогично, при определении углового перемещения в сечении, поворот которого требуется найти, прикладывается пара сил (в плоскости искомого поворота) с моментом, равным безразмерной единице.
Строятся эпюры внутренних силовых факторов от заданной нагрузки и единичных воздействий.
Искомое перемещение определяется из выражения:
правую часть, которого называют интегралами Мора, где: 








Направление единичного воздействия выбирается произвольно. Полученный по формуле (2.1) положительный результат указывает на то, что направление искомого перемещения совпадает с принятым направлением единичного воздействия, либо противоположно принятому направлению, если получен отрицательный результат.
В формуле (2.1) каждый интеграл четко выражает вклад соответствующей деформации в искомое перемещение. Обычно учитываются лишь основные виды деформации. В конструкциях работающих на изгиб учитывается влияние изгибающих моментов, а поперечными силами пренебрегают.
В комбинированных системах, где часть стержней работает на растяжение-сжатие, а часть — на изгиб, учитываются обе эти деформации. В фермах, где каждый стержень работает на растяжение -сжатие в формуле (2.1) остается только первый интеграл.
В случаях, когда ось бруса прямолинейна и жесткость поперечного сечения в пределах отдельных участков постоянна, интегралы
Мора, входящие в выражение (2.1) целесообразно вычислять, используя правило Верещагина или формулу Симпсона.
Возможно вам будут полезны данные страницы:
Пример решения задачи 2.2.
Определить прогиб конца консольной балки (рис. 2.2,а), учитывая лишь деформации, изгиба, жесткость поперечного сечения балки постоянна.
Решение:
Эпюра изгибающих моментов от заданной нагрузки показана на рис.
Построим единичную эпюру, для этой цели, сняв с балки заданную нагрузку, приложим к концу консоли (точка 
вертикально направленную единичную силу 
единичной силы выбирается произвольно , например направим ее вниз, т.е. предполагаем , что точка 
При заданном загружении (рис. 2.2,в), балка имеет один участок 

Подставляя в полученное уравнение прямой координаты начала и конца участка, построим единичную эпюру изгибающих моментов (рис. 2.2, г ).
Для определения прогиба точки 


Перемещение положительно, так как обе сопрягаемые эпюры, лежат по одну сторону от базы ( продольной оси бруса ).
На участке 

Прогиб сечения 
Знак плюс прогиба 
Пример решения задачи 2.3.
Определить угол поворота сечения 
Решение:
Эпюра изгибающих моментов от заданной нагрузки построена ранее в примере, ее вид показан (рис. 2.3, б).
Построим единичную эпюру, для этой цели, сняв с балки заданую нагрузку, приложим в сечении 

Балка имеет три участка. Сопряжение эпюр проведем по участкам. На первом участке (участок 

На втором участке (участок
обе эпюры изгибающих моментов линейны.
Поэтому интеграл Мора на этом участке можно вычислить по формуле трапеций. Применяя ее, найдем:
Полученные выражения отрицательны потому, что знаки ординат «перемножаемых» эпюр 

Получен отрицательный результат потому, что эпюры 


Полученный знак минус указывает на то, что сечение 
Пример решения задачи 3.1.
Для консольной рамы, рис. 3.1,а, определить вертикальное и горизонтальное перемещение точки 

Решение:
Поскольку при определении перемещений в рамах используется интеграл Мора, содержащий изгибающие моменты, построение эпюр 
Построим грузовую эпюру изгибающих моментов, её вид показан на рис. 3.1,6.
Для определения вертикального и горизонтального перемещение точки 


«Перемножим» грузовую и единичные эпюры в пределах длины каждого участка (стержня).

Горизонтальное перемещение точки
Анализируя, полученные выражения, устанавливаем, что точка 
Для определения угла поворота узла 

«Перемножая» грузовую и единичную эпюры, определим угол поворота узла
Сечение поворачивается против хода часовой стрелки.
Пример решения задачи 3.2.
Для шарнирно опертой рамы со стержнями различной жесткости, рис. 3.2,а, определить горизонтальное перемещение точки 
Решение:
Определим опорные реакции от действия заданных нагрузок.
Строим грузовую эпюру изгибающих моментов (рис. 3.2,6).





единичные эпюры изгибающих моментов, см. рис. 3.2,в,г. «Перемножив» эти эпюры с грузовой эпюрой 
Точка 

На странице -> решение задач по сопротивлению материалов (сопромат) собраны решения задач и заданий с решёнными примерами по всем темам сопротивления материалов.
Присылайте задания в любое время дня и ночи в 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназачен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Источник











 обе эпюры изгибающих моментов линейны.
обе эпюры изгибающих моментов линейны.












