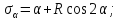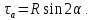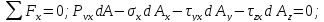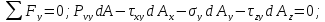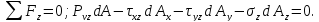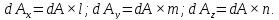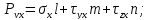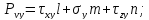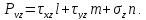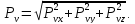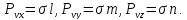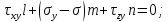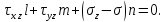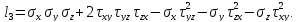Курсовые и лабораторные по по сопромату
Круг Мора моментов инерции сечений
Кроме аналитического метода определения положения главных осей и вычисления главных моментов инерции по формулам (2.8 –2.10) можно использовать графический метод – построение круга Мора моментов инерции сечения. Графический метод может использоваться как независимо, так и для контроля правильности аналитических расчетов. При аккуратном построении круга Мора графический метод позволяет определить положение главных осей и значения главных моментов инерции с точностью 3-х – 5-ти процентов. Круг Мора моментов инерции сечения строится после определения положения центральных осей и вычисления осевых Jy и Jz и центробежного моментов инерции Jyz. При построении круга Мора моментов инерции сечения в прямоугольной системе координат в принятом масштабе на горизонтальной оси откладывают осевые моменты инерции, на вертикальной – центробежный момент инерции:
Порядок построения круга Мора моментов инерции (рис. 2.3).
1. Откладываем на горизонтальной оси осевые моменты инерции Jy — точка 1 и Jz — точка 2;
Из точки 1 по вертикальной оси откладываем (с учетом знака) центробежный момент инерции Jyz. — точка 3; Испытание на кручение образца из малоуглеродистой стали Ц е л ь р а б о т ы: определение модуля упругости второго рода (модуля сдвига), изучение процесса разрушения и определение механических характеристик стали и чугуна при кручении. В инженерной практике на кручение работают валы машин, витые пружины и др. При кручении круглого и кольцевого стержня возникает деформация чистого сдвига.
Делим отрезок 12 пополам – точка 4.
При этом получаем длины отрезков 
между точками ij:
; 
; 
.
4. Из точки 4 проводим окружность радиусом 
.
Получаем точки 5 и 6 пересечения окружности с горизонтальной осью. Длины отрезков от начала координат до этих точек соответственно равны:
;
. (2.12)
Сравнивая Формулы (2.12) с формулами (2.10) главных моментов инерции, видим, что
; 
.
Из рис. 2.3. с учетом формулы (2.8) видно также, что
; 
;
Тогда, из геометрии круга известно, что
и, что отрезки 53 и 63, опирающиеся на диаметр круга, пересекаются под прямым углом.
Следовательно, если вертикальную и горизонтальную оси круга Мора совместить с центральными осями сечения у, z, то направления отрезков 53 и 63 будут совпадать с направлением главных осей сечения.
Таким образом, круг Мора (рис. 2.3) позволяет графически определить величины главных моментов инерции и направление главных осей сечения.
Замечание. Чтобы направления главных осей были получены правильно, необходимо значение центробежного момента инерции откладывать с учетом знака из точки 1 – из конца отрезка 01, равного осевому моменту инерции Jy (момент инерции относительно вертикальной оси).
Эпюры определяют опасное сечение при заданной нагрузке. Линия влияния определяет опасное положение нагрузки для данного сечения. Линии влияния можно строить тремя способами: статическим, кинематическим и деформационным. В этой лекции мы рассмотрели только статический метод.
 |
Линии влияния многопролетных статически определимых балок строятся на основании линий влияния однопролетных балок (рис. 2).
ЗАГРУЗКА ЛИНИЙ ВЛИЯНИЯ
Действие вертикальных сосредоточенных сил
Пусть для однопролетной балки построена линия влияния изгибающего момента в сечении 1 (рис. 3). Тогда для определения изгибающего момента в сечении 1 от действия трех сосредоточенных сил необходимо записать: М1 = F1y1 + F2y2 + F3y3.
В общем виде влияние вертикальных сосредоточенных сил можно учесть при помощи формулы:
(1)
где sk – может быть или изгибающим моментом, или поперечной силой, или опорной реакцией; n – число действующих сосредоточенных сил.
Действие сплошной неравномерно распределенной нагрузки
Пусть на рис. 4, б изображена линия влияния какого либо фактора.
Тогда 
(2)
Если qx = const = q, то из формулы (2) получаем
где А(b,с) – площадь участка линии влияния, вдоль которого распределена нагрузка.
Действие сосредоточенного
Заменим сосредоточенный мо-мент m парой сил
тогда по формуле (1) и согласно рис. 5 имеем:
Источник
7.6. Круг напряжений Мора
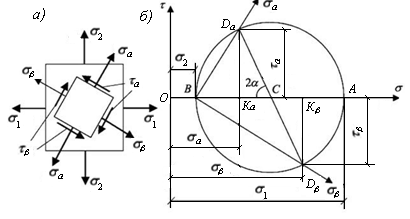
Зависимость напряжений от угла наклона площадки, на которой они действуют, имеет простую геометрическую интерпретацию в виде диаграммы, которая называется кругом напряжений Мора. Обозначим:
Тогда напряжения на наклонных площадках можно представить в виде:
Эти уравнения представляют окружность в параметрической форме. Они эквивалентны уравнению:
Используя круги Мора, можно решать два типа задач.
Первый тип. Пусть известны напряжения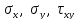 
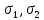
на произволь-ных площадках. Требуется найти главные напряжения 
и положение главных площадок.
Решение. По оси 
(рис. 7.6) отложим отрезок 
, равный по величине 
Рис. 7.6. Схема круга Мора для нахождения главных напряжений
и положения главных площадок
Из точки 
в направлении оси 
отложим отрезок 
соответствующий 
. Аналогично построим точки
, равные напряжениям
. Соединив точки 
, получим точку С пересечения отрезка 
с осью 
. Вокруг точки С опишем окружность диаметром
. Это и будет окружность напряжений Мора.
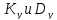
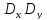
Точки А и В пересечения окружности с осью σ соответствуют главным напряжениям
. Для определения направления главных площадок из точки 
проведем прямую параллельно оси 
до пересечения с окружностью в точке М, которая называется полюсом. Прямые, проведенные из полюса в точки А и В, соответствуют направлению главных напряжений
соответственно.
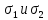
Второй тип. Пусть известны главные напряжения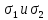
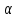
. Требуется определить напряжения на площадках, направленных под углом 
к главным.
Решение. Вдоль оси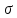 
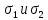
(рис. 7.7, б) отложим отрезки ОА и ОВ, соответствующие главным напряжениям 
. На отрезке АВ, как на диаметре, построим окружность напряжений Мора. Из центра окружности (точка С) отложим центральный угол 2α с осью σ и проведем прямую до пересечения с окружностью в точках Dα и Dβ.
Рис. 7.7. Схема круга Мора для нахождения напряжений
на второстепенных площадках
Координаты этих точек соответствуют напряжениям на площадках, повернутых на угол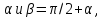 
и на площадке, на которой действует главное напряжение 
. Положения этих площадок получим, проведя из точки В прямые до пересечения с окружностью в точках 
.
7.7. Объемное напряженное состояние
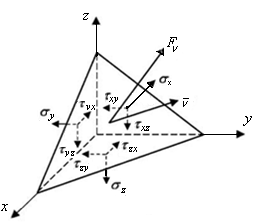
В общем случае напряженного состояния на гранях элементарного параллелепипеда, выделенного в окрестности точки нагруженного тела, действует девять компонентов тензора напряжений. В силу закона парности касательных напряжений независимыми являются только шесть из них.
Вычислим напряжения на произвольной площадке ABC с вектором нормали ν в окрестности произвольной точки О (см. рис. 7.7). Обозначим направляющие косинусы вектора нормали ν к площадке ABC величинами:
Проекции полного напряжения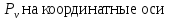
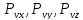
, действующего на площадке АВС, обозначим 
. Для их определения составим уравнения равновесия четырехгранника, выделенного координатными плоскостями и плоскостью АВС в окрестности произвольной точки нагруженного тела (рис. 7.8):
Площади граней элементов связаны между собой зависимостями:
Учитывая это, получим:
Нормальные напряжения найдем, составив сумму проекций на направление нормали:
Полное напряжение на площадке:
Касательное напряжение на площадке:
.
Определение главных напряжений.
Пусть площадка АВС (рис. 7.8) – главная, а нормаль к ней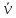 
совпадает с главной осью. Касательные напряжения на этой грани отсутствуют, а нормальное напряжение совпадает с полным. Проекции этого напряжения на координатные оси равны:
Учитывая выражение для 
, получим:
Эти равенства можно рассматривать, как однородную систему линейных алгебраических уравнений относительно l, m и n.
Рис. 7.8. Схема площадки для определения
Так как направляющие косинусы связаны соотношениями l + m + n = 1, нулевое решение этой системы невозможно. Нулевое решение системы возможно только в том случае, когда определитель, составленный из ее коэффициентов при неизвестных, обращается в нуль, т. е.
.
Раскрыв этот определитель, получим кубическое уравнение относительно главного напряжения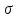 
:
где 
В силу симметрии определителя относительно главной диагонали, соответствующее ему кубическое уравнение имеет три действительных корня, три главных напряжения: 
.
Главные напряжения в точке нагруженного тела не зависят от выбора системы координат. Поэтому
и называют их соответственно первым, вторым и третьим инвариантами тензора напряжений. Их можно представить в виде:
;
;
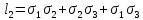
В случае объемного напряженного состояния напряжения также можно представить графически. Если рассмотреть наклонные площадки, параллельные одному из главных напряжений, то для них справедливы формулы для плоского напряженного состояния. Из рис. 7.9 видно, что напряжение σ3 не влияет на величину напряжений σα и τα, действующих на площадке, параллельной σ3. Тогда напряжения на таких площадках можно представить графически, построив круг Мора на главных напряжениях σ1 и σ2. Аналогично можно представить графически напряжения на наклонных площадках, параллельных σ1 и σ2, как показано на рис. 7.10. Однако точки, расположенные на этих трех кругах, не исчерпывают всех наклонных площадок в точке нагруженного тела.
Рис. 7.9. Схема наклонной площадки при объемном
Можно показать, что площадкам общего положения соответствуют точки на плоскости, лежащие в заштрихованной области между тремя кругами Мора. Точки, являющиеся вершинами этих кругов, соответствуют площадкам, наклоненным под углом 45 о к соответствующим главным площадкам.
Рис. 7.10. Круги Мора для определения
Касательные напряжения на этих площадках равны радиусам кругов Мора и определяются формулами:
Максимальное касательное напряжение 
Источник