Поворот сечения интеграл мора

Вопрос 18.Определение перемещений при изгибе. Интеграл Мора. Метод Верещагина.

Прогиб – линейная деформация, смещение центра тяжести поперечного сечения.

Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление.

— перемещение сечения К под действием Р, где M_xp-изгибающий момент в произвольном сечении, _х— единичный момент в том же сечении под действием единичной силы или единичного момента ( если ищется угол поворота), EI_x– жёсткость сечения балки при изгибе.

Правило Верещагина. Используется, когда жёсткость при изгибе постоянна вдоль длины. Эпюра изгибающих моментов должна быть линейной. Максимальный прогиб называется стрелой.

Следует иметь в виду, что способы «перемножения» эпюр применимы только при наличии двух условий:

1.Изгибная жесткость балки на рассматриваемом участке должна быть постоянной(EI=Const),

2.Одна из двух эпюр моментов на этом участке (грузовая или единичная) должна быть обязательно линейной. При этом обе эпюры не должны в пределах данного участка иметь перелома.

Δ_кр= 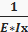* ω_p * _k c — грузовое перемещение

ω_p– площадь грузовой эпюры.

_k c — ордината в единичном эпюре, соответствует центру тяжести грузовой.

При постоянной жесткости по длине балки EI_z для определения прогиба энергетическим методом необходимо вычислять интеграл вида:

.

Допустим, что эпюры изгибающих моментов аналитически выражаются функциями М_z=f₁(х), М ’ _z´ = f₂(х), причем одна из них, например, f₁(х) произвольная, а другая f₂(х) линейная функция и может быть записана в виде f₂(х) = kх+b. Пусть графики этих функций имеют вид представленный на рис. 3.86.

В соответствии с принятыми обозначениями можно записать:

Первый интеграл представляет собой статический момент относительно оси x площади эпюры ограниченной кривой M_z, т.е.

, где

ω – площадь, ограниченная кривой M_z,

х_c — координата центра тяжести фигуры ограниченной кривой M_z относительно оси х.

Второй интеграл представляет собой площадь, ограниченную кривой M_z, которую обозначили ω.

Таким образом, искомый интеграл равен произведению площади эпюры M_z на расположенную под ее центром тяжести ординату эпюры М_z´. Важно отметить, что вычисление перемещения способом Верещагина возможно только в том случае, когда, во-первых, эпюры M_z и М_z´ на рассматриваемом участке не имеют изломов, во-вторых, одна из эпюр описывается линейной зависимостью и именно по ней определяется ордината под центром тяжести другой эпюры y_c. Поэтому при вычислении способом Верещагина интеграл Мора по всей длине балки надо заменить суммой интегралов по участкам, в пределах которых эпюра моментов от единичной нагрузки не имеет изломов. Тогда перемещение сечения балки δ:

Таким образом, для вычисления прогибов по способу Верещагина необходимо:

1) построить эпюру изгибающих моментов от заданных нагрузок M_z (основная эпюра);

2) снять внешнюю нагрузку (но сохранить опоры) и приложить в том сечении, в котором определяется перемещение (угол поворота) единичную силу (единичный момент) в направлении искомого .перемещения (угла поворота);

3) построить эпюру изгибающих моментов от единичной нагрузки М_z´(единичная эпюра);

4) разбить эпюры на участки, в пределах которых отсутствуют изломы эпюр, и для каждого участка вычислить площадь криволинейной эпюры ω_i и ординаты эпюр ограниченных линейной функцией под центрами тяжести криволинейных эпюр у_ci.

5) составить произведения ω_i у_ci и просуммировать:

Встречающиеся на практике эпюры изгибающих моментов разбивают на простейшие фигуры: прямоугольник, треугольник и параболический треугольник.

Площади этих фигур и координаты центров тяжести приведены в таблице

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Определение перемещений. Метод О. Мора в сочетании со способом (формулой) Симпсона

Для определения любого перемещения (линейного или углового) в методе Мора балка рассматривается в двух состояниях: действительном и вспомогательном. Вспомогательное состояние получается следующим образом: сначала всю заданную нагрузку нужно удалить, затем приложить «единичный силовой фактор» в том месте, где требуется определить перемещение, и по направлению этого искомого перемещения. Причем, когда определяем линейное перемещение (прогиб балки), то в качестве «единичного силового фактора» принимается сосредоточенная сила , а если требуется найти угол поворота, то приложить следует сосредоточенную пару .

Далее в одном и том же произвольном сечении обоих состояний (то есть и действительного, и вспомогательного) составляются аналитические выражения изгибающего момента, которые подставляются в формулу, называемую «интегралом Мора»:

где: знак Σ распространяется на все участки балки,

а EI – изгибная жесткость на участке.

Во многих случаях интегрирования по Мору можно избежать и применить способ «перемножения» эпюр. Одним из таких способов является способ Симпсона, по которому значение интеграла Мора на участке длиной ℓ вычисляется по следующей формуле:

Здесь обозначено: a, b и с – соответственно крайние и средняя ординаты эпюры изгибающих моментов действительного состояния М,

— крайние и средняя ординаты эпюры изгибающих моментов, но только вспомогательного состояния .

Правило знаков: если обе «перемножаемые» ординаты в двух эпюрах расположены по одну сторону от оси эпюры (то есть они одного знака), то перед их произведением мы должны поставить знак «плюс: а если они по разные стороны от оси эпюры, то перед произведением ставим знак «минус».

Следует иметь в виду, что способы «перемножения» эпюр (кроме способа Симпсона известен еще способ Верещагина) применимы только при наличии двух условий:

1. Изгибная жесткость балки на рассматриваемом участке должна быть постоянной (EI=Const),
2. Одна из двух эпюр моментов на этом участке должна быть обязательно линейной. При этом обе эпюры не должны в пределах данного участка иметь перелома.

При наличии нескольких участков на балке, удовлетворяющих указанным двум условиям, формула для определения перемещений принимает вид:

Если результат вычисления получается положительным, то, следовательно, направление искомого перемещения совпадает с направлением «единичного силового фактора» ( ), а если результат отрицательный, значит искомое перемещение происходит в направлении, противоположном этому фактору.

Формула Симпсона, записанная через моменты, выглядит следующим образом: перемещения (прогиб или угол поворота) равны

где li – длина участка;

EIi – жесткость балки на участке;

M_F – значения изгибающих моментов с грузовой эпюры, соответственно в начале, в середине и в конце участка;

– значения изгибающих моментов с единичной эпюры, соответственно в начале, в середине и в конце участка.

При перемножении эпюр будет полезным для определения ординат эпюр изгибающих моментов:

Задача

Определить угол поворота сечения на левой опоре φ_А

1) Находим опорные реакции действительного состояния .

2) Строим эпюру моментов действительного состояния М.

3) Выбираем вспомогательное состояние для определения угла поворота φ_А.

4) Находим опорные реакции вспомогательного состояния

«Реагируем» на знак «минус».

5) Строим эпюру моментов вспомогательного состояния:

6) «Перемножаем» эпюры

Поскольку одна из них (а именно ) линейна на всем пролете и не имеет перелома, а эпюра М тоже без перелома, то в формуле Симпсона будет всего один участок, и тогда

Знак «плюс» говорит о том, что сечение А поворачивается в сторону «единичного момента»

Источник