Прямой как моря горизонт

Видимый горизонт и дальность видимости

Расчет видимого горизонта и дальности видимости в зависимости от высоты наблюдателя и наблюдаемого объекта.

Калькулятор ниже предназначен для расчета видимого горизонта и дальности видимости в зависимости от высоты наблюдателя и наблюдаемого объекта. Под ним, как водится, немного теории.

Видимый горизонт и дальность видимости

Видимый горизонт
Так как земля изогнута, наблюдателю, находящемуся, например, в море, представляется, что он находится в центре круга, по краям которого небо как бы смыкается с морской поверхностью. Эта окружность и называется видимым горизонтом наблюдателя. На картинке слева видимый горизонт обозначен пунктирной линией. То есть для наблюдателя, находящегося в точке А на высоте h от земли, видимый горизонт будет образован всеми точками касания лучей зрения земной поверхности (угол BCO равен 90 градусов).

Говоря о видимом горизонте чаще всего имеют в виду длину d отрезка BC. Длину d легко вывести из теоремы Пифагора.

где R — радиус Земли, который обычно принимают за 6378 километров.

В реальной жизни на стороне человека выступает атмосфера. Она, благодаря явлению рефракции, то есть преломлению лучей в верхних слоях атмосферы, расширяет его горизонты примерно на 6% 🙂
Формула, таким образом, принимает вид

В принципе, везде (по крайней мере, насколько я находил в Интернете) для расчетов используют упрощенную формулу, из которой исключен радиус Земли. Она, кстати, вполне выводится из верхней.
, для результата в морских милях или
, для результата в километрах

Дальность видимости
Дальность видимости предметов определяется наибольшим расстоянием, на котором наблюдатель увидит вершину наблюдаемого объекта на линии горизонта. Как видно из рисунка, она зависит как от высоты наблюдателя, так и от высоты наблюдаемого объекта. Собственно, это сумма дальности видимого горизонта наблюдателя и дальности видимого горизонта наблюдаемого объекта. Это довольно важный параметр для навигации.

В калькуляторе я ее вычисляю, а на практике, насколько я понимаю, дальности видимости береговых ориентиров указываются во всяческих лоциях, мореходных таблицах и тому подобном для высоты наблюдателя, равной пяти метрам. Для поправки на фактическую высоту наблюдателя используется «номограмма для расчета дальности видимости предметов в море в дневное время при среднем состоянии атмосферы».

Источник

Сколько километров до горизонта?

Что такое «горизонт»? Мы часто употребляем это слово, например: солнце скрылось за горизонтом или на горизонте показался автомобиль. Но есть ли научное определение данного термина и можно ли измерять расстояние до горизонта?

Что такое горизонт?

Говоря простым языком, это граница между небом и поверхностью земли или воды. Также иногда можно встретить в определении слово «видимый». Горизонт бывает видимым и истинным.

Видимый горизонт – та часть пространства, которую видит наблюдатель, включая границу между небом и земной поверхностью. Истинный горизонт – воображаемый круг небесной сферы, плоскость которого расположена перпендикулярно относительно вертикальной линии в точке наблюдателя. Его также называют астрономическим или математическим.

Видимый и астрономический горизонт

Расстояние измеряется до видимого горизонта. Для этого используется теорема Пифагора и несложная формула:

Чтобы узнать более-менее точное расстояние, необходимо знать две величины: радиус Земли (R) и высоту, на которой находится наблюдатель (h). Таким образом, очевидно, что чем выше располагается наблюдатель, тем сильнее будет отдаляться линия горизонта.

Примеры расстояния от определенного объекта до горизонта:

• человек ростом 1,75 м, стоящий на земле – 4,7 км;
• крыша 8-этажного дома 25 м – 17,9 км;
• воздушный шар 150 м – 43,8 км;
• самолет 10 км – 357,3 км;
• космический корабль 350 км – 2144 км.

Дальность видимости

Если представить, что наблюдатель стоит на ровной поверхности и ничто не загораживает горизонт, то чем ограничен его кругозор? На открытом пространстве линию горизонта ограничивает выпуклость поверхности Земли, связанная с ее геоидной формой.

Предыдущее изображение показывает, что видимость для наблюдателя заканчивается в той точке, где линия горизонта условно пересекается с геоидной формой Земли. Если наблюдатель поднимется выше, его кругозор расширится.

Возникает вопрос, могут ли различные устройства увеличить дальность видимости? Например, способен ли бинокль расширить кругозор в прямом смысле? Поскольку, бинокль – это оптический прибор, он способен лишь увеличить изображение. Для этого он оснащен специальной конструкцией, которая увеличивает отдаленные объекты, делает их более отчетливыми. Но «заглянуть» за линию горизонта при помощи бинокля нельзя.

Конструкция классического бинокля

Горизонт – граница, разделяющая небо и поверхность земли/воды. Расстояние до видимого горизонта зависит от высоты, на которой находится наблюдатель. Чем выше эта точка, тем сильнее отдаляется горизонт. Например, с высоты среднего человеческого роста (1,75 м) расстояние до горизонта составляет 4,7 км.

Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Источник

Что такое линия горизонта?

Каждому известно, что линия горизонта визуально разделяет небесный свод с поверхностью Земли. Горизонт мы видим сферической линией, однако в науке её считают абсолютно прямой. Горизонтальная линия всегда располагается на уровне ваших глаз. Неважно, где и в каком положении вы находитесь, горизонт будет проходить точно перед глазами.

Горизонт не принадлежит к физическим объектам. Линию невозможно достичь и прикоснуться к ней, поскольку она существует только в воображении. Это воображаемая линия, потому её местонахождение полностью зависит от расположения зрителя. Лучше всего горизонт виден на море или в океане. Там он будет границей между небом и водной стихией.

Понятие горизонтальной линии используется географами, астрономами, архитекторами, художниками, дизайнерами и многими другими деятелями. Существуют два понятия горизонта: истинный и видимый. Видимый отдаляется от нас по мере того, как мы поднимаемся над поверхностью. Чем мы выше, тем дальше горизонт. Поднимаясь на высоту, мы пытаемся заглянуть за линию, а она неудержимо убегает.

Истинный горизонт представляет собой воображаемый круг, который располагается на небесной сфере. Чтобы понять, что такое истинный горизонт, расположите перед глазами сосуд с водой. Сосуд должен быть прозрачным, а вода налита наполовину. Теперь поверните его, чтобы вся поверхность жидкости слилась в одну черту. Эта черта и есть истинный горизонт. Он необходим при точном определении месторасположения различных объектов в географии, астрономии и других сферах.

Иногда, сам того не замечая, человек часто ориентируется на линию горизонта. Зрительное восприятие очень связано с этой чертой. Потому её местонахождение всегда учитывают при создании всевозможных изображений. Горизонтальная линия делает его естественным и удобным для созерцания. Любая объёмная проекция начинается с нахождения точки слияния всех линий, идущих к горизонту от наблюдателя.

Художник, рисующий пейзаж, сначала размышляет, где будет находиться горизонтальная черта на картине. В результате этого у полотна будет определённый образ. Если нарисовать горизонт внизу, то наблюдателю будет казаться, что на сюжет картины он смотрит сверху. В пейзаже это придаст ощущение свободы и безмерного простора.

Если линия находится в центре, то зритель будет как бы втянут внутрь картины, при этом создается иллюзия присутствия в сюжете. Если горизонт расположен сверху, то зритель станет всматриваться в передний план, на котором объекты видны достаточно широко, не перегораживая друг друга. Таким образом, чтобы картина была выразительна и приятна для созерцания, следует правильно подойти к выбору линии горизонта.

Источник

Учебник по навигации

Глава 1

§ 6. Видимый горизонт и его дальность

Наблюдатель, находясь в море, всегда видит вокруг себя определенный участок земной поверхности, в центре которого находится он сам. Этот участок принято называть кругозором наблюдателя. Границей кругозора наблюдателя является линия, по которой небосвод как бы соприкасается с морем; называется она линией видимого горизонта. С увеличением высоты глаза наблюдателя его кругозор расширяется, линия видимого горизонта отодвигается от наблюдателя, дальность видимого горизонта увеличивается.
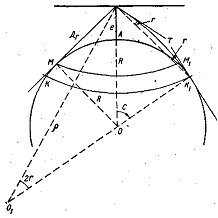
На сферической поверхности Земли линия видимого горизонта представляется малым кругом ММ1 (смотрите рисунок), по которому прямые линии — лучи, проведенные во все стороны от глаза наблюдателя, касаются земной поверхности.
Геометрическая дальность видимого горизонта Дг без учета земной рефракции, представляющая собой сферический радиус AM, может быть рассчитана на основании следующих соображений. Учитывая, что высота глаза наблюдателя е по сравнению с размерами Земли незначительна (на современных кораблях высота глаза едва ли может быть больше 50 м), сферический радиус AM можно считать равным длине касательной ВМ. Тогда из прямоугольного треугольника ОВМ можно написать

Oтношение e / 2R настолько мало, что пренебрежение им практически не скажется на, точности вычисляемой дальности. Учитывая это, можно считать, что

Дг = &#8730 <2re>

Длину сферического радиуса AM и приравненной к нему касательной ВМ мы назвали геометрической дальностью видимого горизонта без учета земной рефракции.

Если бы земная атмосфера во всех своих слоях имела одинаковую плотность (или будь Земля вовсе лишена атмосферы), лучи света от линии видимого горизонта MM1 достигали бы глаза наблюдателя по прямым без искривлений и сферический радиус AM представлял бы фактическую дальность видимого горизонта. В действительности же в земной атмосфере лучи света распространяются не прямолинейно, а с некоторым преломлением вследствие неодинаковой плотности атмосферы в разных ее слоях. Явление преломления светового луча, проходящего через слои земной атмосферы с разной плотностью, называется земной рефракцией. Вследствие рефракции траектория луча, соединяющего малый круг ММ1 с глазом наблюдателя В, в действительности будет кривой линией, обращенной вогнутостью к Земле. Точка касания этого луча с поверхностью Земли будет лежать несколько дальше точки М1, а именно в точке К1. Следовательно, кругозор наблюдателя за счет рефракции расширится и дальность видимого им горизонта увеличится.
Земная рефракция характеризуется углом r земной рефракции, заключенным между хордой ВК1 и касательной к траектории светового луча K1B в точке В. Величина этого угла зависит от преломляющих свойств атмосферы в момент наблюдений, в свою очередь зависящих от разности температуры воды и воздуха, влажности воздуха, атмосферного давления и других факторов. Проходя из более плотных слоев атмосферы у поверхности Земли в менее плотные, на высоте е луч света, преломляясь, искривляется и принимает вид кривой К1В. Поэтому наблюдатель видит точку К1 не по направлению касательной BM1 или хорды BK1, а по направлению касательной ВТ к траектории действительного луча К1В. На сравнительно небольших расстояниях от точки В траекторию луча света можно принять за дугу окружности радиуса &#961 . Из многочисленных наблюдений, произведенных в разное время и в разных частях земного шара, установлено, что отношение R / &#961 , называемое коэффициентом земной рефракции, при нормальном состоянии атмосферы примерно равно 0,16. Этот коэффициент характеризует преломляющую способность земной атмосферы.
Для отыскания зависимости геометрической дальности видимого горизонта с учетом земной рефракции от высоты глаза наблюдателя е обратимся к рисунку. На этом рисунке действительная дальность видимого горизонта Де представлена сферическим радиусом ВК1 малого круга КК1. Вследствие малости кривизны земной поверхности, а тем более зрительного луча практически можно за дальность видимого горизонта принимать как длину сферического радиуса АК1, так и длину хорды ВК1, а также и сферический радиус ВК1. В треугольнике ОК1В угол ВК1О равен 90 градусов минус r , угол К1ВО равен 90 градусов минус (с-r), ВК1 = Де — геометрическая дальность видимого горизонта с учетом земной рефракции.
Применяя к треугольнику ОК1В теорему синусов, можно написать:

ОВ / sin (90&#176 — r) = ОК₁ / sin <90&#176 - (c-r)>
или
R+e / R = cos r / cos (c-r)

Вычтя из правой и левой частей полученного равенства по единице
R+e / R — 1 = cos r / cos (c-r) — 1,
получим
R + e — R / R = cos r — cos (c-r) / cos (c-r);

e / R = cos r — cos (c-r) / cos (c-r).

Заменив в правой части разность косинусов на удвоенное произведение синуса полусуммы на синус полуразности, получим

e / R = 2 sin c/2 sin / cos (c-r)

По малости углов с и r разложим в ряд sin c/2, sin <(c-2r/2>и cos (c-r), ограничившись при этом первыми членами разложения:

sin (c/2) = c/2; sin =c-2r/2; cos (c-r)=1.

Подставляя в предыдущую формулу результаты разложения, найдем

e/r = 2 * c/2(c-2r/2) = c(c-2r)/2

Но c=Д_е/R, а 2r=Д_e / &#961 = Д_еR / R&#961 = (Д_е / R) * k, где
k = R / &#961 — коэффициент земной рефракции.

С учетом последних замечаний

Разложив (1-к) в минус 1/2 степени в ряд и ограничившись двумя первыми членами разложения, получим
Д_е = (1+к/2)* &#8730 <2re>
или
Д_е (мили) = 1,08 * &#8730 <2*6371*е (м) / 1852 * 1852>= 2,08 &#8730 е (м).

Такова формула геометрической дальности видимого горизонта с учетом земной рефракции в море для наблюдателя с высотой глаза, равной е. Для приближенных расчетов можно принимать, что геометрическая дальность видимого горизонта в морских милях равна удвоенному корню квадратному из численного значения высоты глаза наблюдателя в метрах.
В мореходных таблицах имеется специальная таблица 22-а, вычисленная по последней формуле. Пользуясь этой таблицей, можно непосредственно по высоте глаза наблюдателя е выбрать дальность видимого горизонта. Рассмотренные выше геометрические дальности видимого горизонта как с учетом, так и без учета земной рефракции являются дальностями теоретическими. Действительная дальность видимого горизонта в зависимости от условий прозрачности атмосферы может значительно отличаться от теоретической. Действительная дальность видимости может быть определена только опытным путем.

Источник