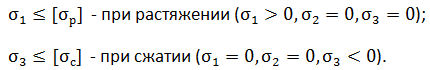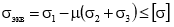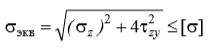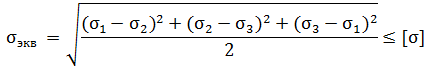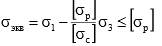Теория прочности мора формула

Теории прочности в сопротивлении материалов.

Важнейшей задачей инженерного курса является оценка прочности детали по известному напряжённому состоянию, т.е. с учётом главных напряжений σ_x, σ_y, σ_z.

Наиболее просто эта задача решается при одноосном напряжённом состоянии.
Условие прочности при одноосном напряжённом состоянии:

В случае двухосного и трёхосного напряжённого состояния необходимо оценивать напряжённое состояние по некоторому критерию прочности, учитывающему действие всех главных напряжений, отличных от нуля.

В соответствие такому критерию устанавливается понятие эквивалентного напряжения .

Эквивалентным называется напряжение одноосного растяжения элемента материала, который равнопрочен тому же элементу при сложном напряжённом состоянии.

Основные теории прочности в сопротивлении материалов.

1.Первая теория прочности ( Гипотеза наибольших нормальных напряжений ).

Опасное состояние материала возникает, когда наибольшее по модулю нормальное напряжение достигает предельного значения соответствующего простому растяжению или сжатию.

где [σ_р] — допускаемое нормальное напряжение при одноосном растяжении; σ_с] — допускаемое нормальное напряжение при одноосном сжатии.

Эта теория дает удовлетворительные результаты лишь для некоторых хрупких материалов (бетона, камня, кирпича) и неприменима для пластичных материалов.

2.Вторая теория прочности ( Гипотеза наибольших относительных удлинений ).

В этой теории в качестве критерия разрушения принято наибольшее по модулю относительное удлинение ε.
Опасное состояние материала наступает тогда, когда наибольшее относительное удлинение достигает опасного значения.

где [σ] — допускаемое нормальное напряжение; µ — коэффициент Пуассона.

Экспериментально эта теория не подтверждается.

3.Третья теория прочности ( Гипотеза наибольших касательных напряжений ) или теория прочности Треска — Сен-Венана.

Причиной разрушения материала считается сдвиг, вызываемый касательными напряжениями. Полагают, что материал разрушается, когда наибольшее касательное напряжение достигает значения, предельного для данного материала.

Теория подтверждается для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию.

4.Четвёртая теория прочности ( энергетическая теория прочности ).

Эта теория предполагает, что пластичный материал находится в опасном состоянии, когда удельная потенциальная энергия формоизменения достигает предельного для данного материала значения.

Теория подтверждается для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию.

5. Теория прочности Мора (пятая гипотеза прочности).

Теория прочности Мора позволяет учесть различное сопротивление материалов растяжению и сжатию.
Например, бетон, который имеет высокую прочность на сжатие, но совершенно не может работать на растяжение.

При [σ_р] = [σ_с] теория прочности Мора совпадает с третьей теорией прочности.

Источник

Сопромат .in.ua

изучаем сопротивление материалов

Теории прочности

Основные теории прочности

Перечислим наиболее известные в сопротивлении материалов теории прочности.

• Первая теория прочности — Теория наибольших нормальных напряжений.
• Вторая теория прочности — Теория наибольших деформаций.
• Третья теория прочности — Теория наибольших касательных напряжений.
• Четвертая теория прочности (энергетическая) — Теория наибольшей удельной потенциальной энергии формоизменения.
• Теория прочности Мора — Теория предельных напряжённых состояний (иногда говорят — V теория прочности).

Из всех вышеперечисленных теорий прочности наиболее полной, точной и всеобъемлющей является теория Мора. Все её положения были проверены экспериментально. Она подходит как для проверки прочности хрупких материалов (чугун, бетон, кирпич), так и для проверки на прочность пластичных материалов (низкоуглеродистая сталь). Теория наибольших нормальных напряжений и теория наибольших деформаций подходит только для прочностного анализа хрупких материалов, причём только для каких-то определённых условий нагружения, если требовать повышенную точность расчёта. Вот поэтому первые две теории прочности сегодня применять не рекомендуется. Результаты теории наибольших касательных напряжений и теории наибольшей удельной потенциальной энергии формоизменения можно получить в некоторых частных случаях нагружения при применении теории Мора.

Общие положения теории прочности

В зависимости от условий нагружения материал может находиться в различных
механических состояниях: упругом, пластическом и в состоянии разрушения. Под предельным подразумевают такое напряженное состояние, при котором происходит качественное изменение свойств материала — переход от одного механического состояния к другому. Для пластических материалов предельным считается напряженное состояние, соответствующее заметным остаточным деформациям, а.для хрупких — такое, при котором начинается разрушение материала.

При линейном напряженном состоянии предельное значение единственного в
этом случае главного напряжения может быть непосредственно определено из опыта (σ_т — для пластических материалов и σ_в — для хрупких). Поэтому оценка прочности в этом частном случае проста. В случае сложного напряженного состояния (объемного или плоского) при оценке прочности необходимо учитывать наличие двух или трех отличных от нуля главных напряжений. При этом опасное состояние материала
зависит не только от величии главных напряжений, но и от соотношений между ними.

Из-за невозможности экспериментального определения критериев опасного состояния материала при сложном напряженном состоянии пользуются гипотезами, формулирующими условия перехода материала в опасное состояние. Па основании таких гипотез построены теории прочности. Эти теории исходят из предпосылок о том, что сложное и линейное напряженные состояния считаются эквивалентными (по прочности), если они при пропорциональном увеличении главных напряжений в одно и то же число раз одновременно становятся опасными. Поэтому оценка прочности материала при любом напряженном состоянии основывается на результатах опытов
при простом растяжении (сжатии), и исследуемое напряженное состояние сравнивается с линейным. Для материалов с выраженной пластичностью за опасное (предельное) состояние принимается такое, при котором начинают развиваться остаточные деформации. Для материалов, находящихся в хрупком состоянии, опасным считается такое состояние, которое предшествует началу появления трещин.

Общая запись условия прочности при сложном напряженном состоянии имеет
вид:

где σ_пр — расчетное или приведенное напряжение при сложном напряженном состоянии.

Формулы приведенных напряжений устанавливаются теориями прочности в
зависимости от принимаемых гипотез.

Первая теория прочности — теория наибольших нормальных напряжений.

Теория наибольших нормальных напряжений — основана на гипотезе о том, что опасное состояние материала наступает тогда, когда наибольшее по абсолютной величине нормальное напряжение достигает значения,
соответствующего опасному состоянию при простом растяжении или сжатии. Приведенные напряжения при объемном напряженном состоянии:

при плоском напряженном состоянии:

Первая теория прочности подтверждается опытами только при растяжении хрупких материалов и лишь в тех случаях, когда все три главные напряжения не однозначны и различны по величине.

Вторая теория прочности

Вторая теория прочности — теория наибольших относительных удлинений исходит из гипотезы о том, что разрушение связано с величиной наибольших относительных удлинений. Следовательно, опасное состояние материала наступает тогда, когда наибольшая по модулю относительная линейная деформация достигает значения, соответствующего опасному состоянию при простом растяжении или сжатии.

В этом случае приведенные напряжения при объемном напряженном состоянии:

$$\sigma_<пр>^ = \sigma_1 – \mu\cdot (\sigma_ <2>+ \sigma_<3>)$$

при плоском напряженном состоянии:

Вторая теория, как и первая, недостаточно подтверждается опытами, что объясняется не учетом особенностей строения реальных тел. Первая и вторая теории прочности отображают хрупкое разрушение путем отрыва (в первой это связывается с σ_макс, втотой — с ε_макс). Поэтому эти теории рассматриваются только как грубое приближение к действительной картине разрушения.

Третья теория прочности

Третья теория прочности — теория наибольших касательных напряжении. В основу теории положена гипотеза о том, что два напряженных состояния — сложное и линейное — эквиваленты в смысле прочности, если наибольшие касательные напряжения одинаковы. Приведенные напряжения при объемном напряженном состоянии:

При плоском напряженном состоянии

Третья теория прочности отображает наступление текучести в материале, а также разрушение путем сдвигов. Она хорошо подтверждается опытами с пластическими материалами, одинаково сопротивляющимися растяжению и сжатию при условии, что главные напряжения имеют разные знаки.

Четвертая теория прочности — энергетическая.

Энергетическая теория прочности (теория наибольшей удельной потенциальной энергии формоизменения) исходит из предпосылки о том, что количество потенциальной энергии формоизменения, накопленной к моменту наступления опасного состояния (текучести материала), одинаково как при сложном напряженном состоянии, так и при простом растяжении. Приведенные напряжения при объемном напряженном состоянии:

или в частном случае при σ_y = 0, полагая σ_x = σ, τ_xy = τ
$$\sigma_<пр>^ = \sqrt<\sigma^2+3\tau^2>$$

Для частного случая чистого сдвига (σ= 0):
$$\sigma_<пр>^ = \tau\sqrt<3>$$

Четвертая теория прочности отображает наступление текучести. Она хорошо подтверждается опытами с пластическими материалами, имеющими одинаковый предел текучести при растяжении и сжатии.

Четвертую теорию прочности часто называют теорией октаэдрических касательных напряжений (октаэдрические касательные напряжения в общем случае определяются по формуле [math]\tau_ <окт>=\frac<1><\sqrt<3>>\cdot\sqrt<(\sigma_1 – \sigma_2)^2+(\sigma_2 – \sigma_3)^2 +(\sigma_3 – \sigma_1)^2>[/math] и к началу развития пластических деформаций при простом растяжении они равны [math]\tau_ <окт>= \frac<\sqrt<2>><3>\sigma_<т>[/math]).

Источник

Обобщённая теория прочности Мора.

Обобщённая теория прочности Мора.

• Обобщенная теория интенсивности Мора. Признавая некоторые отклонения от точной формы, такие как функция, мы упрощаем задачу нахождения предельной плоскости, и, исходя из теории максимального касательного напряжения к нахождению предельной кривой в той же плоскости, условие прочности становится следующим (§ 43), Как известно: Стоимость долговечности условий

нарушения возникновения пластической деформации так и пишет: a1a3-Т, Где SC-максимальное и минимальное основное напряжение. Полученные уравнения можно рассматривать более широко, чем интерпретацию теории максимальных касательных

напряжений, и эти уравнения показывают, что только максимальные и минимальные главные напряжения нарушают долговечность, это Людмила Фирмаль

предположение не совсем верно, и средние главные напряжения A2 также влияют на прочность материала. Однако известно, что этот эффект незначителен, и в крайних случаях погрешность, вызванная падением А2, не превышает 15%, а в большинстве случаев она значительно больше. Если принять это упрощающее предположение, то вместо трехмерного пространства координаты точки представляются главным напряжением, и получается плоскость оси А3. Напряженное состояние материала может быть выражено

в точках с координатами и A3, и может быть более полно нарисовано обобщенной теорией прочности круга§ 251] Mohr 785. Мор, построенный на главных напряжениях Sj и O3, в системе декартовых координат a и t (§ 37). Этот метод отображения напряженного состояния является более полным, поскольку он характеризует величину основного напряжения 0, а также напряженное состояние материала в рассматриваемой точке! Причем не только О3,

• но и напряжения а и Т, действующие на различные участки, проходящие через рассматриваемые точки. Когда это напряжение и А3 вызовет конечное напряженное состояние, если оно достигнет такого значения, 1 постколлегия- Если происходит нарушение определенного вида силы, то соответствующий круг Мора называется пределом. Как использовать 654 относится к пределам круга 1 и 2 при простом растяжении и сжатии для материалов, имеющих различные значения прочности на растяжение и сжатие(чугун). Длина

АО представляет собой прочность на растяжение, а OV — прочность на сжатие. Измените предельное напряженное состояние с простого растяжения на простое сжатие, уменьшите положительный Gj от нуля до нуля и увеличьте отрицательный g3 от нуля до S (по абсолютной величине). Перед промежуточным предельным напряженным состоянием существует непрерывная серия предельных кругов Мора. При ступенчатом переходе от окружности 1 к окружности 2 Эта серия окружностей дает кривую, показанную на рисунке. 654 пунктирная линия, которая является конвертом

для семей, чтобы ограничить круг торгового центра. Эта огибающая Людмила Фирмаль

является предельной кривой, которая заменяет набор кривых/2 и L и Li / 1, а касательная каждого молярного круга к этой кривой (в соответствии со свойством огибающей) является предельной кривой. Фактически, в верхней части огибающей окружность Мора изменяется на точку, и поэтому напряжения at и A3, а следовательно, и IA2, равны друг другу. С другой стороны, предельная кривая остается открытой, так как невозможно разрушить материал равномерным всесторонним сжатием. Когда пределы прочности на растяжение и сжатие равны (сталь), огибающая является началом координат, параллельным горизонтальной оси (фиг. 655). На практике это

происходит потому, что чаще встречаются напряженные состояния, нарисованные кругами Мора, расположенными между 1 и 2. 654), соответствующие части огибающей просто заменяются прямыми линиями, касательными к этим окружностям. Если вы уменьшите масштаб чертежа на коэффициент K, который является коэффициентом запаса k, вы не получите ограниченный круг мола, но вы получите круг, который указывает допустимую прочность материала[CHAP. XXXVIII Напряженное состояние. Как использовать 656 простое натяжение натяжение натяжение [a_] с простым сжатием. Какой-то средний Сегмент OA является

приемлемым[0(растягивающее напряжение) сдвиг начинается при меньшем значении тангенциального напряжения t, чем при a

Изучу , оценю , оплатите , через 2-3 дня всё будет на «4» или «5» !

Откройте сайт на смартфоне, нажмите на кнопку «написать в чат» и чат в whatsapp запустится автоматически.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник