Зависимость атм давления от высоты над уровнем моря

Как с высотой изменяется атмосферное давление. Формула, график

Не все знают, что на разной высоте давление атмосферы отличается. Существует даже специальный прибор для измерения и давления, и высоты. Называется он барометр-альтиметр. В статье мы подробно изучим, как с высотой изменяется атмосферное давление и при чем тут плотность воздуха. Рассмотрим эту зависимость на примере графика.

Давление атмосферы на разных высотах

Атмосферное давление зависит от высоты. При ее увеличении на 12 м давление уменьшается на 1 мм ртутного столба. Этот факт можно записать с помощью такого математического выражения: ∆h/∆P=12 м/мм рт. ст. ∆h — это изменение высоты, ∆P — изменение атмосферного давления при изменении высоты на ∆h. Что из этого следует?

Из формулы видно, как с высотой изменяется атмосферное давление. Значит, если мы поднимемся на 12 м, то АД уменьшится на 12 мм ртутного столба, если на 24 м — то на 2 мм ртутного столба. Таким образом, измеряя атмосферное давление, можно судить о высоте.

Миллиметры ртутного столба и гектопаскали

В некоторых задачах давление выражается не в миллиметрах ртутного столба, а в паскалях или гектопаскалях. Запишем вышеприведенное соотношение для случая, когда давление выражено в гектопаскалях. 1 мм рт. ст. =133,3 Па =1,333 гПа.

Теперь выразим соотношение высоты и атмосферного давления не через миллиметры ртутного столба, а через гектопаскали. ∆h/∆P=12 м/1,333 гПа. После вычисления получим: ∆h/∆P=9 м/гПа. Выходит, что когда мы поднимаемся на 9 метров, то давление уменьшается на один гектопаскаль. Нормальное давление — это 1013 гПа. Округлим 1013 до 1000 и примем, что на поверхности Земли именно такое АД.

Если мы поднимаемся на 90 м, как с высотой изменяется атмосферное давление? Оно уменьшается на 10 гПа, на 90 м — на 100 гПа, на 900 м — на 1000 гПа. Если на земле давление в 1000 гПа, а мы поднялись на 900 м вверх, то атмосферное давление стало нулевым. Так что, получается что атмосфера заканчивается на девятикилометровой высоте? Нет. На такой высоте есть воздух, там летают самолеты. Так в чем же дело?

Связь плотности воздуха и высоты. Особенности

Как с высотой изменяется атмосферное давление вблизи поверхности Земли? На этот вопрос уже ответила картинка выше. Чем больше высота, тем меньше плотность воздуха. Покуда мы находимся недалеко от поверхности земли, изменение плотности воздуха незаметно. Поэтому на каждую единицу высоты давление уменьшается примерно на одно и тоже значение. Два записанные нами ранее выражения нужно воспринимать как правильные, только если мы находимся недалеко от поверхности Земли, не выше 1-1,5 км.

График, показывающий как атмосферное давление изменяется с высотой

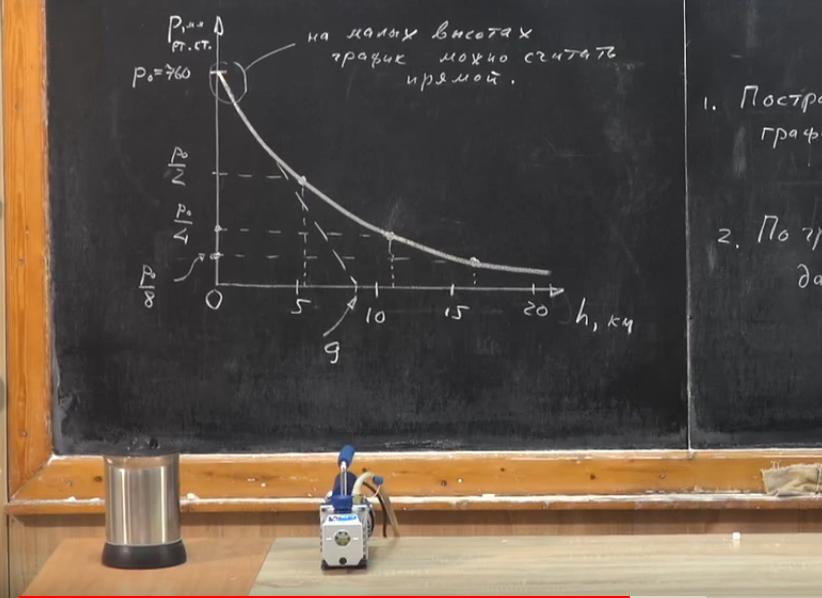
Теперь перейдем к наглядности. Построим график зависимости давления атмосферы от высоты. При нулевой высоте P₀=760мм рт. ст. Из-за того, что с ростом высоты давление уменьшается, атмосферный воздух будет менее сжат, его плотность станет меньше. Поэтому на графике зависимость давления от высоты не будет описываться прямой линией. Что это значит?

Как с высотой изменяется атмосферное давление? Над поверхностью земли? На высоте 5,5 км оно уменьшается в 2 раза (Р₀/2). Оказывается, что если мы поднимемся еще на такую же высоту, то есть на 11 км, давление уменьшится еще вдвое и будет равно Р₀/4 и т. д.

Соединим точки, и мы увидим, что график — это не прямая, а кривая. Почему, когда мы записывали соотношение зависимости, складывалось впечатление, что на высоте 9 км атмосфера заканчивается? Мы считали, что график является прямой на любых высотах. Это было бы так, если бы атмосфера была жидкой, то есть если бы ее плотность была постоянной.

Важно понимать, что этот график является лишь фрагментом зависимости на малых высотах. Ни на какой точке этой линии давление не снижается до нуля. Даже в глубоком космосе существуют молекулы газов, которые, правда, не имеют отношение к земной атмосфере. Ни в одной точке Вселенной не существует абсолютного вакуума, пустоты.

Источник

Зависимость давления от высоты: барометрическая формула

Многие люди знают, что с увеличением высоты уменьшается давление воздуха. Рассмотрим вопрос, почему давление воздуха уменьшается с высотой, приведем формулу зависимости давления от высоты, а также рассмотрим пример решения задачи с использованием полученной формулы.

Что такое воздух?

Воздух — это бесцветная смесь газов, которая составляет атмосферу нашей планеты. В его состав входят множество различных газов, основными из которых являются азот (78 %), кислород (21 %), аргон (0,9 %), углекислый газ (0,03 %) и другие.

С точки зрения физики поведение воздуха при существующих условиях на Земле подчиняется законам идеального газа — модели, согласно которой молекулы и атомы газа не взаимодействуют друг с другом, расстояния между ними огромные по сравнению с их размерами, а скорости движения при комнатной температуре составляют порядка 1000 м/с.

Давление воздуха

Рассматривая вопрос зависимости давления от высоты, следует разобраться, что представляет собой концепция «давление» с физической точки зрения. Под давлением воздуха понимают силу, с которой воздушный столб давит на поверхность. В физике она измеряется в паскалях (Па). 1 Па означает, что сила в 1 ньютон (Н) перпендикулярно приложена к поверхности площадью 1 м 2 . Таким образом, давление 1 Па — это очень маленькое давление.

На уровне моря давление воздуха составляет 101 325 Па. Или, округляя, 0,1 МПа. Это значение принято называть давлением 1 атмосферы. Приведенная цифра говорит, что на площадку 1 м 2 воздух давит с силой 100 кН! Это большая сила, однако человек ее не ощущает, так как внутри него кровь создает аналогичное давление. Кроме того, воздух относится к текучим веществам (к ним также относятся жидкости). А это значит, что он оказывает по всем направлениям одинаковое давление. Последний факт говорит о том, что давление атмосферы с разных сторон на человека взаимно компенсируется.

Зависимость давления от высоты

Атмосферу около нашей планеты держит земная гравитация. Гравитационные силы также являются виновником падения давления воздуха с увеличением высоты. Справедливости ради следует отметить, что не только земное притяжение приводит к уменьшению давления. А также снижение температуры тоже вносит свой вклад.

Поскольку воздух является текучим веществом, тогда для него можно использовать гидростатическую формулу зависимости давления от глубины (высоты), то есть ΔP = ρ*g*Δh, где: ΔP — величина изменения давления при изменении высоты на Δh, ρ — плотность воздуха, g — ускорение свободного падения.

Учитывая, что воздух является идеальным газом, из уравнения состояния идеального газа следует, что ρ = P*m/(k*T), где m — масса 1 молекулы, T — его температура, k — постоянная Больцмана.

Объединяя две приведенные выше формулы и решая полученное уравнение относительно давления и высоты, можно получить следующую формулу: P_h = P₀*e -m*g*h/(k*T) , где P_h и P₀ — давление на высоте h и на высоте уровня моря, соответственно. Полученное выражение называется барометрической формулой. Она может использоваться для расчетов зависимости атмосферного давления от высоты.

Иногда для практическим целей необходимо решать обратную задачу, то есть находить высоту, зная давление. Из барометрической формулы легко можно получить зависимость высоты от уровня давления: h = k*T*ln(P₀/P_h)/(m*g).

Пример решения задачи

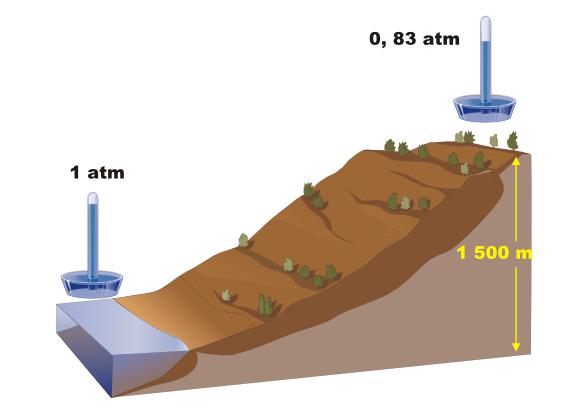
Боливийский город Ла-Пас является самой «высокой» столицей в мире. Из разных источников следует, что город расположен на высоте от 3250 метров до 3700 метров над уровнем моря. Задача состоит в расчете давления воздуха на высоте Ла-Пас.

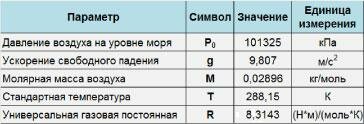
Для решения задачи воспользуемся формулой зависимости давления от высоты: P_h = P₀*e -m*g*h/(k*T) , где: P₀ = 101 325 Па, g = 9,8 м/с 2 , k = 1,38*10 -23 Дж/К, T = 293 K (20 o C), h = 3475 м (среднее между 3250 м и 3700 м), m = 4,817*10 -26 кг (с учетом молярной массы воздуха 29 г/моль). Подставляя цифры, получаем: P_h = 67 534 Па.

Таким образом, давление воздуха в столице Боливии составляет 67 % от давления на уровне моря. Низкое давление воздуха является причиной головокружений и общей слабости организма, когда человек поднимается в горные районы.

Источник

Зависимость давления воздуха от высоты

Многие люди, особенно альпинисты, пастухи на горных пастбищах, знают, что с увеличением высоты уменьшается давление воздуха. Становится трудно дышать, невозможно сварить горячую пищу, чай. Естественно, появляется вопрос: почему давление воздуха уменьшается с высотой? Рассмотрим решение этого вопроса.

Что такое воздух? Воздух — это бесцветная смесь различных газов, составляющих атмосферу нашей планеты. Основными газами, из которых состоит воздух, являются азот (78 %), кислород (21 %), аргон (0,9 %), углекислый газ (0,03 %) и другие. С точки зрения физики поведение воздуха при существующих условиях на Земле подчиняется законам идеального газа. Согласно этой модели молекулы и атомы газа не взаимодействуют друг с другом, расстояния между ними огромные по сравнению с их размерами, а скорости движения при комнатной температуре по расчетам по молекулярно-кинетической теории газов составляют порядка 460 м/с.

Что такое «давление» с физической точки зрения.

Под давлением воздуха понимают силу, с которой воздушный столб давит на поверхность. В физике она измеряется в паскалях (Па). 1 Па означает, что сила в 1 ньютон (Н) перпендикулярно приложена к поверхности площадью 1 м2. Поэтому давление 1 Па — это очень маленькое давление. На уровне моря давление воздуха составляет примерно 0,1 МПа (точнее -101 325 Па), что соответствует давлению 1 атмосфера. Это значит, что на площадку 1 см2 воздух давит с силой 1 кгс, а на площадку 1 м2 – 100 х 100 =10’000 кгс = 10 тонно-силы (или 100 кН)! Это очень много, но человек ее не ощущает, так как внутри него каждая клетка создает аналогичное противодавление. Последний факт говорит о том, что давление атмосферы с разных сторон на человека взаимно компенсируется.

Кстати, если внезапно возле человека убрать давление воздуха, то он взорвется! По настоящему. По этой причине водолазы с большой глубины должны подниматься достаточно медленно, чтобы жидки составляющие организма (например, кровь) не вскипели.

Зависимость давления от высоты

Атмосферу около нашей планеты существует за счет земной гравитации. Эти же силы являются виновниками падения давления воздуха с увеличением высоты. Но не только земное притяжение приводит к уменьшению давления. Снижение температуры тоже вносит свой вклад. Основная причина, по которой изменяется давление с высотой, заключается в том, что на каждый последующий слой воздуха давит меньшее количество воздуха. На поверхности Земли давлению в 1 атм. Соответствует тот факт, что весь столб воздуха площадью в 1 см2 от поверхности Земли и до далекого космоса весит 1 кг. Для расчета изменения давления воздуха с высотой можно использовать гидростатическую формулу зависимости давления от глубины (высоты). Изменение этого давления можно определить по формуле

где: dP — величина изменения давления при изменении высоты на dh,
ρ — плотность воздуха,
g — ускорение свободного падения.

Из уравнения состояния идеального газа можно получить, что

ρ = P * m / (k * T), (2)

где m — масса 1 молекулы,
T — его температура,
k — постоянная Больцмана.

Объединяя две приведенные выше формулы и решая полученное уравнение относительно давления и высоты, можно получить следующую формулу:

где Ph и P₀ — давление на высоте h и на высоте уровня моря, соответственно,
P₀ = 101 325 Па,
g = 9,8 м/с² ,
k = 1,38*10^-23 Дж/К,
m = 4,817*10^-26 кг (с учетом молярной массы воздуха 29 г/моль),
^ — знак возведения в степень.

Подставляя известные значения в (3):

m * g / k =4,817*10^-26 кг*9,8 м/с² / 1,38*10^-23 Дж/К = 34,2 *10^-3 = 0,0342,

ее можно переписать в окончательном виде:

Ph = P₀ *e-m*g*h/(k*T) → 101 325 * e^-0,0342*h/T (4)

Полученное выражение может использоваться для расчетов зависимости атмосферного давления от высоты и температуры (постоянной на любой высоте) называется барометрической формулой. Для примера рассчитаем давление воздуха на вершине горы Джомолунгма (или – Эверест) в Китае на Гималайских горах на высоте 8848 м.

Для решения задачи воспользуемся формулой (4) зависимости давления от высоты. Для расчетов примем следующие значения неизвестных параметров:

T = 293 K (20 ℃),
h = 8848 м,

Подставляя эти числа в (4), получаем:

Ph = 101 325 *e^-0,0342*8848/293 = 101 325 *e^-1,0327 = 36076 Па, (5)

Это значение почти в три раза меньше, чем на уровне поверхности моря.

Если хотите узнать, что обозначает слово или словосочетание, в ОПЕРЕ выделите это слово(сочетание), нажмите правую клавишу мыши и выберите «Искать в . «, далее — «Yandex». Если это текстовая ссылка – выделите ее, нажмите правую клавишу мыши, выберите «перейти …». Все! О-ля-ля!

Если вам понравилась статья, то поставьте «лайк» и подпишитесь на канал! Если не понравилась – все равно комментируйте и подписывайтесь. Этим вы поможете каналу. И делитесь ссылками в ваших соцсетях!

Источник

Зависимость атм давления от высоты над уровнем моря

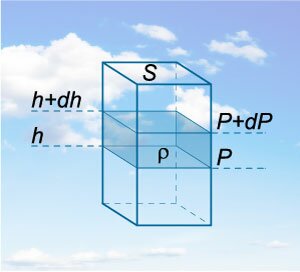
В данном разделе мы выведем зависимость давления газа \(P\) от высоты \(h\) над уровнем моря в гравитационном поле Земли.

Возьмем произвольную цилиндрическую колонну газа с площадью сечения \(S\) и высотой \(h.\) Вес выделенного объема газа будет равен \[F = mg = \rho gV = \rho ghS,\] где \(\rho\) означает плотность газа. Плотность газа будет выражаться следующей формулой: \[\require P = \frac = \frac<<\rho gh\cancel>><\cancel> = \rho gh. \] Теперь представим такую колонну в атмосфере и выделим в ней тонкий слой воздуха высотой \(dh\) (рисунок \(1\)). Ясно, что такой слой вызывает изменение давления на величину \[dP = — \rho gdh.\] Мы поставили здесь знак минус, поскольку давление должно уменьшаться с увеличением высоты.

Рассматривая атмосферный воздух как идеальный газ, воспользуемся уравнением Менделеева-Клапейрона, чтобы выразить плотность \(\rho\) через давление \(P:\) \[ RT,>\;\; <\Rightarrow P = \frac<>RT = \frac<\rho >RT.> \] Здесь \(T\) − абсолютная температура, \(R\) − универсальная газовая постояная, равная \(8.314\,<\large\frac<\text<Дж>>>\normalsize>,\) \(M\) − молярная масса, которая для воздуха равна \(0.029\,<\large\frac<\text<кг>><\text<моль>>\normalsize>.\) Отсюда следует, что плотность определяется формулой \[\rho = \frac<><>.\] Подставляя это в дифференциальное соотношение для \(dP,\) находим: \[ ><>gdh,>\;\; <\Rightarrow \frac<>

= — \frac<><>dh.> \] В результате мы получаем дифференциальное уравнение, описывающее давление газа \(P\) как функцию высоты \(h.\) Интегрирование приводит к следующему уравнению: \[ <\int <\frac<>

> = — \int <\frac<><>dh> ,>\;\; <\Rightarrow \ln P = - \frac<><>h + \ln C.> \] Избавляясь от логарифмов, получаем так называемую барометрическую формулу \[P = C\exp \left( < - \frac<><>h> \right).\] Константа \(C\) определяется из начального условия \(P\left( \right) = ,\) где \(\) − это среднее атмосферное давление над уровнем моря.

Таким образом, зависимость атмосферного давления от высоты выражается формулой: \[P = \exp \left( < - \frac<><>h> \right).\] Подставляя известные стандартные значения (смотрите рисунок \(2\) выше), находим зависимость \(P\left( h \right)\) (в килопаскалях), которая описывается формулой \[ ><<8.3143 \cdot 288.15>>h> \right) > = <101.325\exp \left( < - 0.00012\,h>\right)\;\left[\text <кПа>\right],> \] где высота \(h\) над уровнем моря выражается в метрах.

Если давление определяется в миллиметрах ртутного столба \(\left( \text <мм.рт.ст.>\right),\) то барометрическая формула принимает вид: \[P\left( h \right) = 760\exp \left( < - 0.00012\,h>\right)\;\left[ \text <мм.рт.ст.>\right].\] Барометрическая формула широко используется для оценки атмосферного давления при различных условиях, хотя она дает слегка завышенные значения.

Давление воздуха в шахте можно оценить, используя общую барометрическую формулу : \[P = \exp \left( < - \frac<><>h> \right).\] Подставим в эту формулу следующие значения: \(h = — 1000\,\text<м>\) (знак минус соответствует расположению ниже уровня моря), \(T = 40 + 273.15 = 313.15\,\text<К>.\) Остальные параметры являются стандартными: \(M = 0.02896\,\large\frac<\text<кг>><\text<моль>>\normalsize,\) \(R = 8.3143\,\large\frac<\text<Н>\cdot\text<м>><\text<моль>\cdot\text<К>>\normalsize,\) \(g = 9.807\,\large\frac<\text<м>><\text<с>^2>\normalsize.\)

После несложных вычислений находим: \[

\exp \left( < - \frac<><>h> \right) > = <\exp \left[ < - \frac<<0.02896 \cdot 9.807>><<8.3143 \cdot 313.15>>\left( < - 1000>\right)> \right] > \approx <\exp \left( <0.109>\right) > \approx <1.115.> \] Поскольку атмосферное давление на уровне моря составляет \( = 760\;\text<мм.рт.ст.>,\) то давление воздуха в шахте будет равно \(848\;\text<мм.рт.ст.>,\) что примерно на \(12\%\) выше стандартного давления на уровне моря.

Источник